Die kinetische Gastheorie

Während wir in der Thermodynamik überhaupt nicht nach dem Aufbau der uns umgebenden Materie fragen, machen wir uns jetzt ein konkretes Modell und versuchen, daraus einige Eigenschaften der Materie zu berechnen.

Die kinetische Theorie beruht auf drei Voraussetzungen:

(1) Ein Gas besteht aus Teilchen mit der Masse m und dem Durchmesser d, die sich ständig in ungeordneter Bewegung befinden.
(2) Die Teilchen sind vernachlässigbar klein, d.h. ihre Durchmesser sind viel kleiner als der Weg, den ein Teilchen im Mittel zwischen zwei Stößen zurücklegt.
(3) Die Teilchen verhalten sich wie starre Kugeln, d.h. sie erleiden elastische Stöße, wenn der Abstand ihrer Zentren gleich d wird.

Die Stöße bewirken, dass die Teilchen ständig ihre Geschwindigkeit und ihre Bewegungsrichtung ändern. Die Stoßzahl z gibt an, wie viele Stöße ein Teilchen im Mittel in der Zeiteinheit erleidet. Die mittlere freie Weglänge λ ist der Weg, den ein Teilchen im Mittel zwischen zwei Stößen zurücklegt. Wir können die zweite Voraussetzung deshalb so formulieren: d << λ. Weil man jede beliebige mechanische Größe als Kombination von Größen mit den Dimensionen Masse, Länge und Zeit ausdrücken kann und weil m, λ, und 1/z diese Dimensionen haben, kann man aus ihnen durch geeignete Kombinationen jede beliebige mechanische Größe eines Gases berechnen.

Wir stellen uns nun vor, dass sich unser Gas in einem quaderförmigen Behälter befindet, und untersuchen, welche Wirkung die Stöße der Gasmoleküle auf die zur y, z-Ebene parallele Wand mit der Fläche A haben.

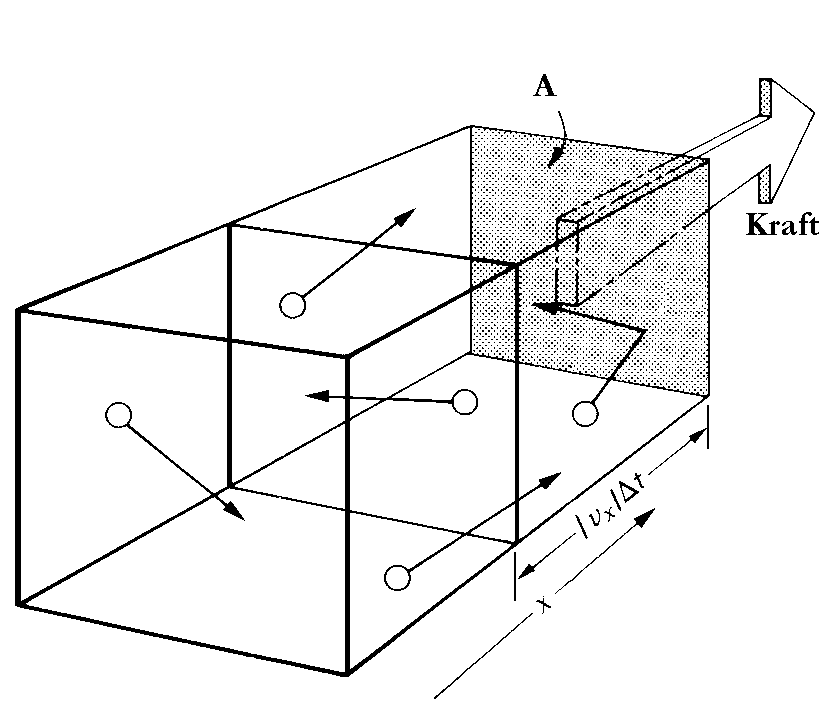Abb. 1: Bei der Berechnung des Gasdrucks geht man von der Kraft aus, die von den auf die dunkle Wand  treffenden Teilchen ausgeübt wird. Im Zeitintervall Δt treffen alle Teilchen auf die Wand, die sich innerhalb des Volumens A  ≥ vx ≥Δt  befinden und sich in Richtung der Wand bewegen. Beim Stoß an die Wand wird das Vorzeichen der x-Komponente ihres Impulses gerade umgekehrt.

Von den Molekülen, die sich in x-Richtung auf die Wand A zu bewegen, fliegt die Hälfte auf die Fläche A zu (die andere Hälfte in Richtung der gegenüberliegenden Wand). In einer bestimmten Zeitspanne dt werden von diesen Molekülen nur diejenigen auf die Wand treffen, die zu Beginn dieser Zeitspanne höchstens um die Strecke |v_x|dt von A entfernt waren, wenn v_x die Geschwindigkeit der Teilchen in x-Richtung ist. Ist Ñ die Teilchendichte der Gasteilchen (Teilchen pro Volumen), so ist die Zahl der Stöße während der Zeit dt auf A:  ¹/₂ÑAv_xdt. Jedes Teilchen der Masse m hat vor dem Stoß den Impuls mv_x, nach dem Stoß einen Impuls gleicher Größe, aber entgegengesetzter Richtung. Deshalb überträgt jedes Teilchen beim Stoß einen Impuls der Größe 2mv_x auf die Wand. Der während der Zeit dt auf die Fläche A insgesamt übertragene Impuls dp_x ist dann

Nun ist aber die Ableitung des Impulses nach der Zeit nichts anderes als die Kraft F_x = ^dpx /_dt und die durch die Fläche dividierte Kraft der Druck p = F/A, so dass sich aus der Kombination der Gleichungen

wobei das Symbol < > angibt, dass es sich um einen Mittelwert handeln soll, da nicht alle Teilchen die gleiche Geschwindigkeit haben müssen. Da v² = v_x²+v_y²+v_z² ist und die Mittelwerte <v_x²>, <v_y²> und <v_z²> aufgrund der Isotropie des Raumes (keine Raumrichtung ist bevorzugt) gleich sein müssen, gilt: <v²> = <v_x²>+<v_y²>+<v_z²> = 3<v_x²>, oder für den Druck p:

p = ¹/₃ Ñm<v²>

Die Teilchendichte Ñ ist gleich N/V, wobei N die Anzahl der Teilchen im Volumen V ist. Mit  N = n N_A  (N_A ist die Loschmidtsche, bzw. Avogadro-Konstante) gilt dann

Durch Vergleich mit der Zustandsgleichung für das perfekte Gas (pV = nRT= nN_AkT) ergibt sich
 

(k = R/N_A). Wir erhalten also eine Beziehung für die quadratisch gemittelte Geschwindigkeit der Teilchen in Abhängigkeit von der Temperatur.
Daraus folgt

Daraus erkennen wir, dass Wärme eine Art von Bewegung der Teilchen sein muss. Für T gegen Null verschwindet die kinetische Energie, d.h. die Teichen kommen zur Ruhe. Diesen Zustand kann man nicht exakt erreichen; mit Hilfe von Laserlicht ist es jedoch möglich, Atome oder Moleküle nahe an den absoluten Nullpunkt zu bringen (T=2µK). Dafür gab es 1997 den Nobelpreis. Durch weitere Verbesserung der Laserkühlung gelang es Temperaturen um 100 nK zu erzielen, was zur so genannten "Bose-Einstein-Kondensation", einem neuen Zustand der Materie führte. Hierfür gab es 2001 den Nobelpreis.

Bringen wir zwei ideale Gase unterschiedlicher Molekülmassen miteinander in Kontakt, so stellt sich nach einiger Zeit das thermische Gleichgewicht ein, d.h. beide Gase nehmen die gleiche Temperatur an. Dann muss aber auch die mittlere kinetische Energie aller Gasteilchen gleich groß sein, d.h. es muss gelten

Das Verhältnis der mittleren Geschwindigkeiten der Moleküle zweier verschiedener miteinander im thermischen Gleichgewicht stehender Gase ist umgekehrt proportional der Wurzel aus dem Verhältnis ihrer Molekülmassen. Wenn die Moleküle zweier unterschiedlicher Gase im thermischen Gleichgewicht dieselbe kinetische Energie E_kin besitzen, dann stimmen bei gleichen Drücken die molaren Volumina der beiden Gase überein, das bedeutet, dass in gleichen Volumina die gleiche Stoffmenge bzw. die gleiche Anzahl von Teilchen enthalten ist, d.h. wir erhalten das Avogadrosche Gesetz.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.