Wenn wir irgendwelche Stoffe aus ihrer Lösung oder Schmelze ungestört kristallisieren lassen, dann bilden sie unter gegebenen Bedingungen stets dieselbe Kristallform; diese ist zugleich ein Bild der räumlichen Anordnung der Moleküle, Ionen oder Atome, die den Kristall bilden. Der Übergang vom amorphen in den kristallinen Zustand erfolgt spontan und - mindestens bei niedermolekularen Substanzen - innerhalb eines sehr engen Temperaturbereichs. Auch bei Abkühlung in die Nähe des absoluten Nullpunktes geht die Materie in keinen anderen Zustand mehr über; ein vollkommener Einkristall stellt also unter gegebenen Bedingungen den Zustand der niedrigsten inneren Energie dar.
Der Nachweis der Kristallinität ist das Kriterium für das Vorliegen eines Stoffes im festen Zustand; fest und kristallin sind daher in strengen Sinne synonym. Da die Unnachgiebigkeit und Formbeständigkeit fester Körper den Sinnen unmittelbar zugänglich ist, bezeichnen wir allerdings auch oft solche Stoffe als fest, bei denen der innere Ordnungszustand nicht ohne weiteres definierbar ist (Gläser, Polymere usw.).
Die Beugung von Wellen ist die Grundlage für eine Reihe leistungsfähiger Methoden zur Bestimmung der Struktur von Molekülen und Festkörpern. Röntgenstrahlen haben Wellenlängen, die mit den Abständen der Atome in Kristallen vergleichbar sind (ca. 100 pm); sie werden deshalb an Kristallgittern gebeugt. Die Intensitätsmuster der gebeugten Röntgenstrahlen geben ein genaues Bild von der Lage der Atome selbst in so komplizierten Molekülen wie den Proteinen. Elektronen mit Geschwindigkeiten von 20000 kms-1 (nach Beschleunigung in einem Potentialgefälle von etwa 4 kV) haben Wellenlängen von 40 pm und eignen sich deshalb ebenfalls für Beugungsuntersuchungen. Auch Neutronen, die in einem Kernreaktor erzeugt und auf thermische Energien abgebremst werden, haben ähnliche Wellenlängen und werden oft eingesetzt.
Die Betrachtung vieler Kristalle führt zu der Erkenntnis, dass man sie aufgrund ihrer äußeren Form in sieben Kristallsysteme einteilen kann. Die Zuordnung zu den Kristallsystemen erfolgt so, dass man die Winkel zwischen den Kristallflächen misst und prüft, wie viele Achsen zur Beschreibung der Kristallform erforderlich sind. Braucht man z.B. drei zueinander senkrechte, äquivalente Achsen, dann gehört der betreffende Kristall zum kubischen System.
Man kann die Kristallsysteme anhand ihrer Symmetrieelemente behandeln.
Das kubische System hat z.B. vier dreizählige Achsen und drei
vierzählige, das monokline System dagegen u.a. eine zweizählige
Achse.
| Kristallsysteme | Achsen | Winkel | Kristallklassen | |
| Bezeichnung nach Schoenflies | Internationale Bezeichnung
(Hermann-Mauguin) |
|||
| triklin | a; b; c | α;β;γ | C1, Ci | 1,1 |
| monoklin | a; b; c | α = γ = 90°; β | Cs, C2, C2h | m, 2, 2/m |
| orthorhombrisch | a; b; c | α = β = γ = 90° | C2v, D2, D2h | 2mm, 222, mmm |
| rhomboedrisch
(trigonal) |
a = b = c | α = β = γ | C3, C3v, D3, D3h, S6 | 3, 3m, 32, 62m, 3 |
| tetragonal | a = b; c | α = β = γ = 90° | C4, C4v, C4h, D2d, D4, D4h, S4 | 4, 4mm, 4/m, 422, 42m, 4/mmm, 4 |
| hexagonal | a = b; c | α = β = 90°;
γ = 120° |
C6, C6v, C6h, C3h, D3d, D6, D6h | 6, 6mm, 6/m, 6, 3m, 622, 6/mmm |
| kubisch
(regulär) |
a = b = c | α = β = γ = 90° | T, Td, Th, O, Oh | 23, 43m, m3, 43, m3m |
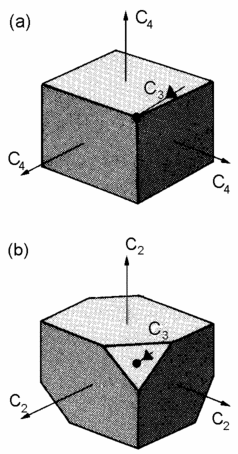 |
| Abb. 1: Diese beiden Kristalle gehören zum kubischen System, sie unterscheiden sich aber in den zusätzlichen rotatorischen Symmetrieelementen: (a) hat vierzählige Achsen, (b) zweizählige. Sie gehören damit zu verschiedenen Kristallklassen. |
Bei der Bestimmung der Kristallklassen tritt ein Problem auf: Die verschiedenen Kristallflächen wachsen mit unterschiedlicher Geschwindigkeit; dadurch kann die äußere Form des Kristalls erheblich von dem Idealbild abweichen. Wenn wir die Kristallklassen eindeutig festlegen wollen, müssen wir daher die inneren Symmetrieelemente eines Kristalls erkennen.
Ein Kristall ist eine regelmäßige Anordnung von Teilchen; in einem gewissen Sinn ist diese Anordnung symmetrisch. Bevor wir mit einer genauen Beschreibung der Kristallstrukturen beginnen, haben wir eine Reihe von Begriffen zu definieren:
(1) Die asymmetrische Einheit ist das Teilchen (Atom, Ion oder
Molekül), aus dem der Kristall aufgebaut ist.
(2) Das Raumgitter ist eine dreidimensionale Anordnung von Punkten,
die alle in gleicher Weise von Nachbarn umgeben sind. Damit definiert das
Raumgitter die Grundstruktur des Kristalls. In manchen Fällen befindet
sich an jedem Gitterpunkt eine asymmetrische Einheit. Das muss aber
nicht sein: Es kann z.B. jeder Gitterpunkt das Zentrum eines Aggregates
aus drei asymmetrischen Einheiten sein. Im Prinzip ist das Raumgitter das
abstrakte Gerüst einer Kristallstruktur.
(3) Die Kristallstruktur erhält man, wenn man jedem Gitterpunkt
ein Aggregat aus asymmetrischen Einheiten zuordnet, die symmetrisch und
für jeden Gitterpunkt in gleicher Weise angeordnet sind.
(4) Die Elementarzelle ist die Grundeinheit, aus der der ganze
Kristall lediglich durch translatorische Verschiebung konstruiert werden
kann (ähnlich wie Ziegelsteine in einer Wand).
Die Elementarzelle muss die Symmetrie des Kristalls haben.
Die Morphologie des Kristalls hängt, wie schon erwähnt, von den unterschiedlichen Wachstumsgeschwindigkeiten der verschiedenen Kristallflächen ab; allen Formen liegt aber die gleiche Struktur der Elementarzelle zugrunde. Wenn wir die Symmetrieelemente der Elementarzelle bestimmen können, ist es uns möglich, den Kristall eindeutig zu klassifizieren.
Nicht jeder der Punktgruppen, die es bei Molekülen gibt, ist auch
für Elementarzellen erlaubt, denn die Elementarzellen müssen
so aufgebaut sein, dass sie lückenlos zu unendlich ausgedehnten
Strukturen zusammengesteckt werden können. Diese Bedingung reduziert
die Anzahl der zulässigen Symmetriegruppen ganz erheblich. Bei einem
zweidimensionalen Gitter gibt es z.B. nur fünf Formen, mit denen man
eine Ebene lückenlos füllen kann; diese Formen sind rotationssymmetrisch
und haben die Symmetrie Cn mit n = 1, 2, 3, 4 und 6. Andere
Rotationssymmetrien kann es nicht geben; das hängt damit zusammen,
dass es prinzipiell unmöglich ist, einen Boden mit regelmäßigen
Fünfecken (n = 5) oder mit Polygonen mit n >6 zu bedecken.
Im dreidimensionalen Raum gibt es vierzehn Typen von Elementarzellen,
mit denen man den Raum lückenlos füllen kann; sie heißen
Bravais-Gitter (Abbildung 2). Man nennt die Elementarzellen , bei
denen sich nur an den Ecken Gitterpunkte befinden, primitive Gitter
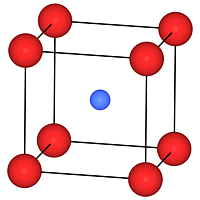
und bezeichnet sie mit P; eine raumzentrierte Elementarzelle (I)
hat einen Gitterpunkt im Zentrum, und eine flächenzentrierte Elementarzelle
(F) hat Gitterpunkte auf ihren Flächen. Es ist bemerkenswert, dass
die Bravais-Gitter sieben Gruppen bilden, von denen jede durch ein primitives
Gitter repräsentiert wird, und dass diese sieben regelmäßigen
Figuren genau den sieben Kristallsystemen entsprechen. Das bedeutet; die
sieben Kristallsysteme geben gerade die sieben Körper wieder, mit
denen man den Raum lückenlos füllen kann; darüber hinaus
ist die Existenz der Kristallklassen eine Folge des Vorkommens der entsprechenden
Symmetrieelemente in den Elementarzellen. Deshalb weist die Tetraederform
eines Kristalls auf eine Elementarzelle mit Tetraedersymmetrie hin usw.
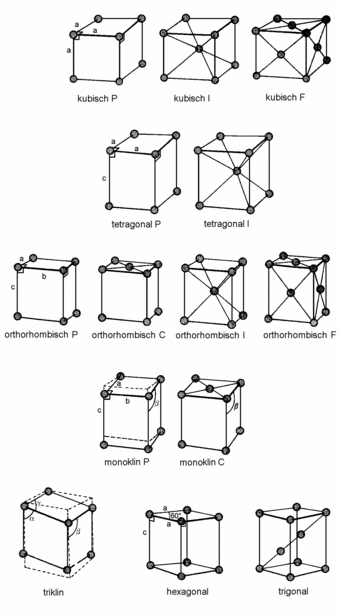 |
| Abb. 2: Die vierzehn Bravais-Gitter. Die kleinen Kreise sind die Gitterpunkte; sie müssen nicht unbedingt von Atomen besetzt sein. Eine primitive Elementarzelle wird mit P bezeichnet, eine raumzentrierte mit I, eine flächenzentrierte mit F und eine Zelle mit Gitterpunkten auf zwei Flächen mit C. |
Wenn wir die Symmetrie der Elementarzellen kennen, können wir daraus sofort auf die Eigenschaften des Festkörpers schließen. Wollen wir z.B. wissen, ob ein Kristall optisch aktiv ist, haben wir nur darauf zu achten, dass die Elementarzelle keine Drehspiegelachse hat. Die Elementarzelle des Quarzes hat die Symmetrie 32 (T nach Schoenflies) und ist deshalb optisch aktiv. Andererseits hat die Elementarzelle des Calcits die Symmetrie 3m (D3d) und ist folglich nicht optisch aktiv. Bei einer vollständigen Analyse der Symmetrieeigenschaften von Kristallen muss man sowohl ihre Symmetrie bezüglich einer Translation als auch die Symmetrie der einzelnen Elementarzellen berücksichtigen. Das führt zur Theorie der Raumgruppen, die wir Spezialisten überlassen wollen.
Max von Laue vermutete 1912, dass Röntgenstrahlen bei Durchtritt
durch einen Kristall gebeugt werden, da deren Wellenlänge vergleichbar
mit den Abständen der Atome in einem Kristall ist. Beugung erfolgt,
wenn Wellen miteinander interferieren. Sind ihre Amplituden in Phase, so
verstärken sie sich gegenseitig und bewirken eine erhöhte Intensität.
Sind die Amplituden nicht in Phase, so löschen sie sich gegenseitig
aus und die Intensität wird geringer.
Jetzt wollen wir uns ein ganzes Paket von reflektierenden Gitterebenen ansehen (Abbildung 3)
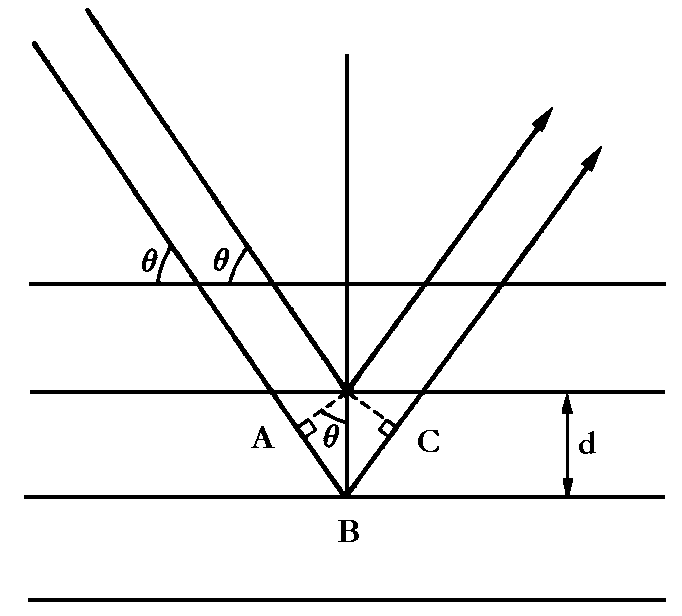 |
| Abb.3: Üblicherweise behandelt man nach Bragg jede Gitterebene als eine Ebene, die die ankommende Strahlung reflektiert. Die Weglängen unterscheiden sich um die Strecke AB + BC, die von dem Winkel Θ abhängt. Konstruktive Interferenz (ähnlich einer einfachen Reflektion) erfolgt, wenn AB + BC ein ganzzahliges Vielfaches der Wellenlänge ist. |
Die Weglängendifferenz zwischen den beiden Strahlen ist AB + BC, und das ist gleich 2d sin Θ, wobei d der Abstand der Gitterebenen und Θ der so genannte Glanzwinkel ist. Für die meisten Glanzwinkel ist die Wellenlängendifferenz kein ganzzahliges Vielfaches der Wellenlänge, und damit wird die Interferenz destruktiv (auslöschend). Wenn die Wellenlängendifferenz dagegen genau ein ganzzahliges Vielfaches der Wellenlänge ist (d.h. wenn AB + BC = n·λ gilt), so sind die reflektierten Wellen in Phase und interferieren konstruktiv. Man wird also eine helle Reflektion beobachten, wenn der Glanzwinkel die Braggsche Bedingung erfüllt:
nλ = 2d sinΘ.
Die Braggsche Bedingung ist die Grundlage der Röntgen-Kristallographie, bei der die innere Struktur von Kristallen mit Hilfe von Röngenstrahlen untersucht wird. Sie ermöglicht in erster Linie die Bestimmung der Abstände zwischen den Gitterebenen, denn wenn man den Winkel Θ, der einem Intensitätsmaximum entspricht, kennt, läßt sich d leicht berechnen.
Ein anderes Verfahren wurde von Debye und Scherrer und unabhängig
von ihnen von Albert Hull entwickelt. Sie untersuchten pulverförmige
Proben mit monochromatischen Röntgenstrahlen. Ein Pulver ist ein ungeordneter
Haufen winziger Kristalle; in ihm wird immer ein Teil der Körnchen
für eine vorgegebene monochromatische Strahlung die Braggsche Bedingung
erfüllen. Die Pulvermethode eignet sich gut für die qualitative
Analyse einer Probe und für eine erste Abschätzung der Größe
und Symmetrie einer Elementarzelle; sie kann aber natürlich nicht
mit der Braggschen Methode konkurrieren, bei der mit monochromatischen
Röntgenstrahlen genaue Informationen über die Elektronendichteverteilung
in einem Kristall gewonnen werden können.
Ergebnisse der Röntgenstrukturanalyse
Zwischen den Teilchen in einem Kristall gibt es Bindungen verschiedenster Art. Die einfachste Bindung liegt im Prinzip in Metallen vor, in denen ein regelrechter Elektronensee in dem Gitter aus identischen Kationen fließt und das Ganze regelrecht zu einer festen, aber doch duktilen Struktur verbindet. Die Kristallstrukturen der Metalle ergeben sich überwiegend aus den Möglichkeiten, kugelförmige Metallkationen möglichst dicht zusammenzupacken.
In Ionenkristallen wird die Kristallstruktur überwiegend durch das geometrische Problem bestimmt, wie man Ionen unter Berücksichtigung ihrer Größe und ihrer Coulomb-Wechselwirkungen in einer möglichst energiearmen Anordnung zusammenbauen kann.
In kovalenten Kristallen werden die Atome durch ein Netz von kovalenten Bindungen, das sich durch den ganzen Kristall erstreckt, in einer bestimmten räumlichen Anordnung festgehalten. Dabei spielen die stereochemischen Anforderungen, die sich aus der Richtungsabhängigkeit der Valenzen ergeben, eine größere Rolle als das einfache geometrische Problem einer Kugelpackung, und es können komplizierte und ausgedehnte Strukturen entstehen. Ein bekanntes Beispiel ist der Diamant, in dem jedes sp3-hybridisierte Kohlenstoffatom tetraedrisch mit vier Nachbarn verbunden ist. Materialien mit solchen Strukturen sind oft sehr hart und wenig reaktionsfähig. In der Mitte zwischen den Extremfällen der kovalenten und der Ionenkristalle stehen die Silikate; bei ihnen tritt eine Mischung aus kovalenten und ionischen Bindungen auf (sowohl zwischen den Silikatgruppen und den Kationen als auch innerhalb der SiO4-Gruppen aufgrund des großen Unterschiedes zwischen den Elektronegativitäten von Silizium und Sauerstoff).
Molekülkristalle entstehen, wenn diskrete Moleküle aufgrund ihrer Van-der-Waals-Wechselwirkungen aneinander gebunden werden. Die Kristallstruktur ist dann das Ergebnis der Aufgabe, Teilchen verschiedener Größe so zu einem Aggregat zu kondensieren, dass die Freie Enthalpie möglichst klein wird. Es ist allerdings nur in Ausnahmefällen möglich, eine Kristallstruktur vorauszuberechnen. Wenn Wasserstoffbrücken auftreten, wird das ganze Problem noch komplizierter; dabei wirkt ein Proton als Verbindungsglied zwischen zwei elektronegativen Atomen. Es gibt Substanzen, wie z.B. Eis, bei denen Wasserstoffbrücken die Kristallstruktur dominieren. In anderen Fällen, z.B. beim Phenol, deformieren sie die durch die Van-der-Waalsschen Wechselwirkungen bestimmte Struktur. Kristalle, deren Struktur zwischen molekularem und kovalentem Charakter liegt, findet man bei Polymeren: Deren lange Ketten werden aus Monomeren durch Ausbildung neuer kovalenter Bindungen gebildet, aber für die Anordnung und Anziehung zwischen den Ketten sind Van-der-Waalssche Wechselwirkungen verantwortlich. Je einheitlicher die Längen der Polymermoleküle sind, um so kristalliner und dichter ist der Festkörper.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.