Maxwellsche Geschwindigkeitsverteilung

Wir haben jetzt alle Voraussetzungen entwickelt, um die Verteilung der Komponenten der Teilchengeschwindigkeiten in einem perfekten Gas herleiten zu können. Die drei Komponenten v_x, v_y und v_z sind voneinander unabhängig, deshalb ist die Wahrscheinlichkeit, dass ein Teilchen eine Geschwindigkeit mit Komponenten zwischen v_x und v_x + dv_x und v_y und v_y + dv_y und v_z und v_z + dv_z hat, gleich dem Produkt der einzelnen Wahrscheinlichkeiten:

Wir bringen jetzt ein, dass die Geschwindigkeitsverteilung F(v) raumsymmetrisch sein soll, dass also F(v) nur von der Geschwindigkeit v und nicht von den einzelnen Komponenten v_x,v_y und v_z abhängen soll. Beispielsweise soll eine Geschwindigkeit mit den Komponenten v_x = 0,2 km/s; v_y = 0,3 km/s und v_z = 0,6 km/s, also dem Betrag v = (0,2² + 0,3² + 0,6²)^1/2 = 0,7 km/s, gleich wahrscheinlich sein, wie eine Geschwindigkeit mit dem Komponenten v_x = 0,6, v_y = 0,2 und v_z = 0,3 km/s oder irgend eine andere mit v = 0,7 km/s. Weil F demnach nur von v² = v_x² + v_y² + v_z² abhängen soll, schreiben wir einfach

Diese Gleichung kann nur von einer Exponentialfunktion erfüllt werden, denn es ist e^x+y+z = e^xe^ye^z. Wir können also direkt schreiben

wobei die Konstanten a und b noch zu bestimmen sind. Die Lösung erfüllt unsere Bedingung

Die Zweideutigkeit des Vorzeichens ist schnell beseitigt: Die Wahrscheinlichkeit darf nicht ins Unendliche wachsen, es kommt also nur das negative Vorzeichen in Frage. Die Konstanten a und b lassen sich wie folgt berechnen. Da jedes Teilchen irgendeine Geschwindigkeit zwischen -∞ und +∞ haben muss, gilt:
 

Wir erhalten:

Es ist also a = (b/π)^½ und damit

Die Größe b bestimmen wir über den Mittelwert von v_x²   :

Das Integral ergibt ¹/₂(π/b³)^½ und daher

Wir kennen bereits <v_x²>, denn es gilt ja

Da im Mittel die Beiträge bzgl. x,y,z gleich sein müssen, gilt

d.h. <v_x²> = kT/m. Man nennt dies das Gleichverteilungsgesetz.
Nach Einsetzen in die obige Gleichung <v_x²> = ½ b = ^kT/_m gewinnen wir

und die vollständige Formel für die Verteilung der Geschwindigkeitskomponenten lautet:
 

Man nennt diese Gleichung die Maxwell-Boltzmann-Verteilung der Molekülgeschwindigkeiten (Hier etwas über Clerk Maxwell und Ludwig Boltzmann).
Mit Hilfe der hochauflösenden Spektroskopie kann diese Geschwindigkeitsverteilung über den Doppler-Effekt indirekt nachgewiesen werden.
Die Verteilung der Teilchengeschwindigkeiten ohne Berücksichtigung ihrer Richtung erhält man in der folgenden Weise. Die Wahrscheinlichkeit, dass ein Teilchen Geschwindigkeitskomponenten zwischen v_x und v_x + dv_x und v_y und v_y + dv_y und v_z und v_z + dv_z hat, ist gegeben durch:

Wie müssen nun noch das Volumenelement dv_xdv_ydv_z, was einen Quader mit den Seitenlängen dv_x, dv_y und dv_z entspricht, in ein Volumenelement umrechnen, welches nur von v abhängt. Dies ist einfach die Kugelschale (4πv²) mit dem Radius v und der Dicke dv:

So ergibt sich
 

Das ist die sogenannte Maxwell-Verteilung der Molekülgeschwindigkeiten (Originalveröffentlichung).
 

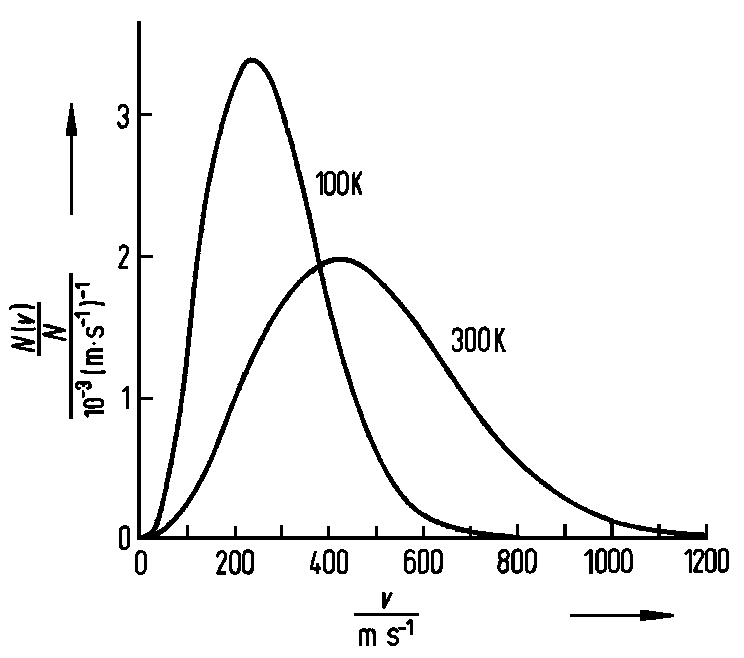Abb. 1: Geschwindigkeitsverteilung für Stickstoff bei verschiedenen Temperaturen

 

Eigenschaften der Maxwell-Verteilung:

Die Maxwellsche Geschwindigkeitsverteilung ist in der Abb. für N₂ bei  T = 100 K und  T = 300 K dargestellt.  Man erkennt, dass die Verteilung bei höheren Temperaturen breiter wird und dass die wahrscheinlichste Geschwindigkeit v_m (definiert durch das Maximum der Verteilungskurve) bei höheren Temperaturen zu größeren Werten verschoben ist. v_m erhalten wir aus der Extremwertbestimmung von F(v):
 

Sie unterscheidet sich ein wenig von der quadratisch gemittelten Geschwindigkeit
 

 Die mittlere Geschwindigkeit <v> erhalten wir durch Auswerten des Integrals  <v>= _o∫^∞vF(v)dv:
 

Bei leichteren Teilchen sind die mittleren Geschwindigkeiten größer als bei schweren Teilchen; die Tabelle enthält einige Zahlenwerte:
 

Noch mehr über Maxwell

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.