Plasma

Plasmen

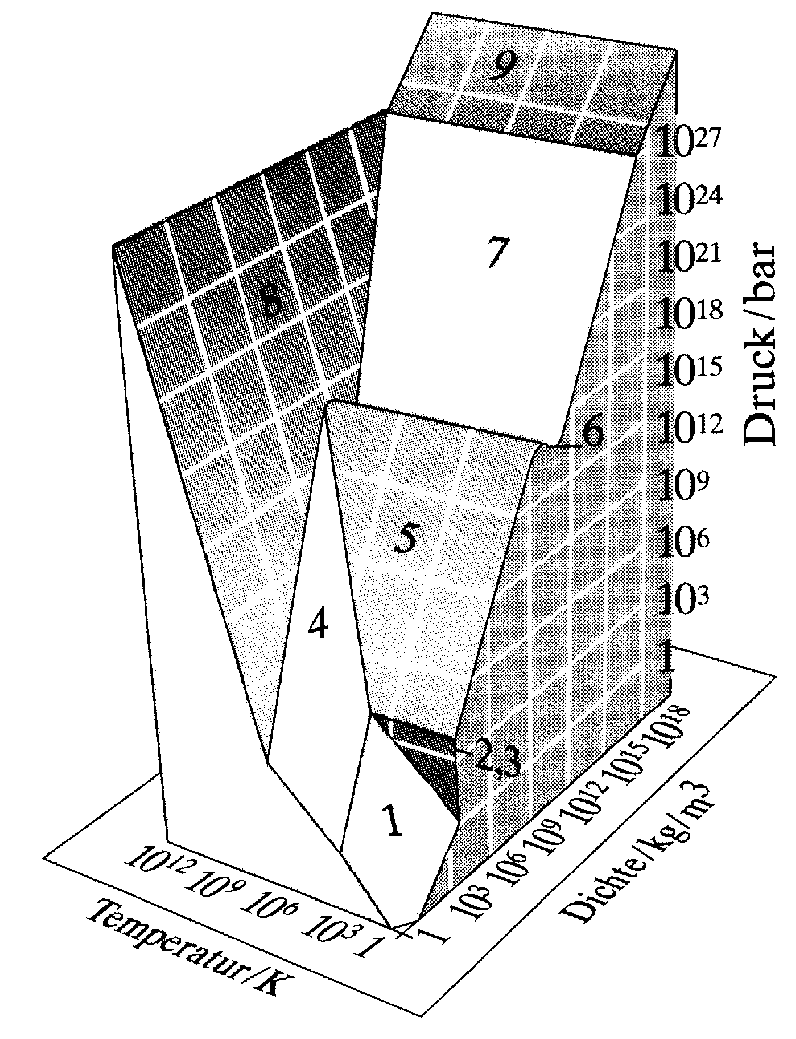Abb. 1: Zustandsflächen der acht Aggregatzustände (die Übergänge sind schematisiert, weil das Modell keinen speziellen Stoff, sondern das ungefähre Verhalten aller Stoffe darstellen soll; z.B. ist der van der Waals - Maxwell - Übergang gasförmig-kondensiert nicht erkennbar).
(1): Gas; (2, 3): flüssig-fest; (4): Plasma; (5): Elektronen - Fermi-Gas; (6): Relativistisches Fermi-Gas; (7): Neutronengas; (8): Photonengas; (9): Relativistisches Neutronengas-Schwarzes Loch

Mit steigender Temperatur schließt sich an die drei klassischen Aggregatzustände ein vierter, der Plasmazustand an. Der größte Teil der Materie im Weltall ist hochionisiert, ist ein Plasma. Man kann aus Gasatomen oder -molekülen Elektronen abtrennen, also diese Teilchen ionisieren, indem man thermische, optische, elektrische oder kinetische Energie zuführt. Wir betrachten hier zunächst die thermische Ionisation durch Stoß mit anderen Gasteilchen.
Die Ablösearbeit E_i eines Elektrons vom Atom oder Molekül, also die Ionisierungsenergie, liegt in der Größenordnung 10 eV (etwas weniger bei Metallen, besonders Alkalien, etwas mehr bei Nichtmetallen). Auch hier haben bei hinreichend hoher Temperatur einige Teilchen im Schwanz der Maxwell-Verteilung genügend hohe kinetische Energien, um stossionisieren zu können. Im thermischen Gleichgewicht ergibt sich der Ionisierungsgrad, d.h. ein für ein festes Volumen betrachtetes Verhältnis der Ionenzahl n_i zur Gesamtteilchenzahl n aus der Boltzmann-Verteilung: Die n_i ionisierten Teilchen liegen energetisch mindestens um E_i höher als die n₀ = n-n_i Teilchen, die ihr Elektron noch besitzen (mindestens um E_i, weil Elektron und Ion auch kinetische Energie haben können). So geht der Faktor e^-Ei/(kT) in die so genannte Eggert-Saha-Gleichung ein. Sie beschreibt für schwache Ionisation von Plasmen den relativen Anteil geladener Teilchen, d.h. Elektronen und ionisierter Atome. In ihr steht der Faktor g_i/g₀ für die statistischen Gewichte (Wahrscheinlichkeitssummen) von Elektron-Ion-Paar und neutralem Teilchen.

Natürlich gibt es keinen scharfen Übergang zwischen Gas und Plasma, aber nach der Eggert-Saha-Gleichung steigt der Ionisationsgrad in einem Bereich von einigen 1000 K von fast 0 auf fast 1. Bei sehr hohem Druck kommt man noch zu weiteren Aggregatzuständen, in denen die Materie ganz neue Eigenschaften entwickelt (Abb. 1): Zum Fermi-Gas, zum relativistischen Fermi-Gas, zum Neutronengas.

Plasmen sind im wesentlichen quasineutral, enthalten also gleich viele positive wie negative Ladungen. Trennung und Isolierung makroskopischer Mengen geladener Teilchen würde ja so ungeheure Kraft erfordern, wie sie nirgends verfügbar ist. Lokale Abweichungen von der Quasineutralität in mikroskopischen Bereichen sind dagegen die Regel. Rings um jede positive Ladung überwiegen die negativen als Debye-Hückel-Wolke und umgekehrt. Sind Atome mit hoher Elektronenaffinität (Halogene, Chalkogene usw.) vorhanden, dann lagern sich die von den positiven Ionen abgespaltenen Elektronen an sie an. Das Plasma besteht dann aus Ionen beider Vorzeichen. Bei höheren Temperaturen, wenn die Ionisierung die Außenschalen aller Atome erfasst, gibt es nur noch positive Ionen und Elektronen. Wegen ihrer geringen Masse bewegen sich die Elektronen viel schneller als die Ionen, sowohl thermisch als auch im elektrischen Feld. Sie fliegen durch ein praktisch unbewegliches Ionengitter, das allerdings im Unterschied zum Festkörper ungeordnet ist. Daher bestehen enge Beziehungen zwischen Plasma- und Festkörperphysik.

Ein Plasma besteht aus mindestens drei Teilsystemen: Dem Elektronengas, dem Ionengas und dem Neutralgas, wozu man noch das "Gas" der Photonen des emittierten Lichts rechnen kann. Durchaus nicht immer stehen alle Teilsysteme untereinander im thermischen Gleichgewicht, selbst wenn innerhalb jedes Systems ein solches Gleichgewicht herrscht. Dementsprechend kann jedes Teilsystem seine eigene Temperatur haben. Das ist typisch für Gasentladungen. Die Energie aus der äußeren Spannungsquelle teilt sich zunächst den Elektronen mit und geht erst allmählich auf die Ionen und noch viel unvollständiger auf das Neutralgas über.

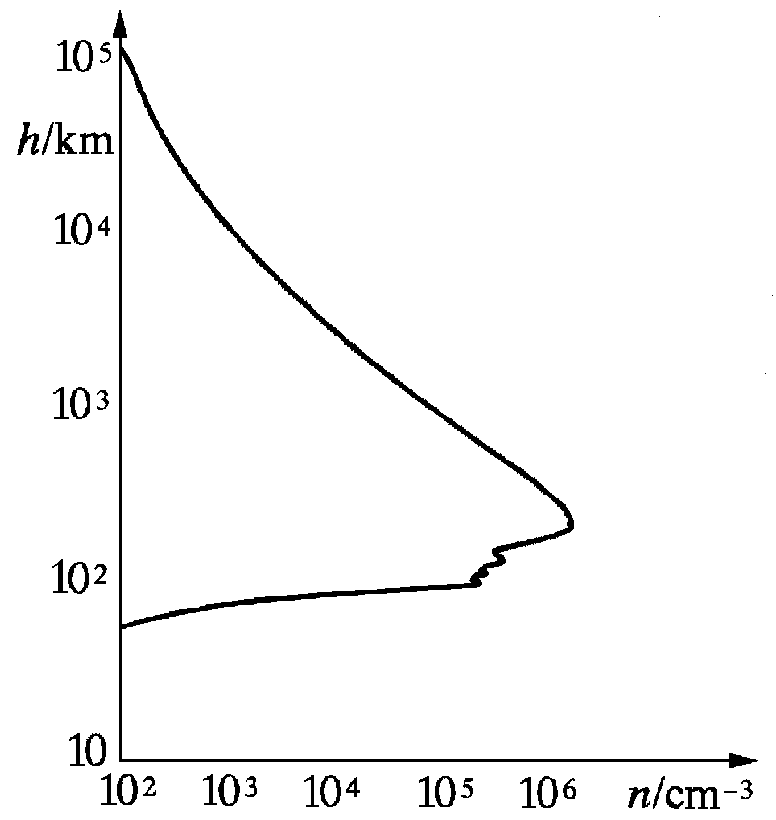Abb. 2: Elektronendichte in der Atmosphäre als Funktion der Höhe zu einer Zeit relativ starker Ionisation.

Neben der thermischen ist auch die Ionisation durch Licht von Bedeutung. Sie tritt durch kurzwellige Anteile der Sonnenstrahlung (vom mittleren UV bis ins weiche Röntgengebiet) in den oberen Schichten unserer Erdatmosphäre auf und führt zur Dissoziation der Luftbestandteile (O₂, O, N₂, NO) und erzeugt damit in relativ dünnen Höhenzonen hohe Elektronen- und Ionenkonzentrationen n_e bzw. n_i, die so genannte Ionosphäre. Jede dieser Schichten, die einem bestimmten Ionisierungsprozess entspricht, hat ein scharfes Maximum in der Höhenverteilung von n_e(Abb. 2). Das Maximum und seine Schärfe kommen deswegen zustande, weil schon einige Dutzend Kilometer oberhalb davon zu wenige ionisierbare Teilchen da sind (exponentieller Abfall der Dichte mit der Höhe), während schon einige km darunter die zur Ionisierung fähigen Strahlungskomponenten eben infolge dieser Ionisierungsprozesse zu schwach geworden ist. So ergeben sich, besonders bei Tage, Elektronenkonzentrationen bis zu 10⁷/cm³, die nachts infolge der Rekombination auf 10⁵/cm³ bis 10⁶/cm³ abfallen. Beiderseits des Maximums sind natürlich auch kleinere Elektronenkonzentrationen anzutreffen. Dies hat drastischen Einfluss auf den Funkverkehr. Der klassische Funkverkehr (Lang-, Mittel- und Kurzwelle) wäre ohne die Ionosphäre überhaupt nicht möglich. Eine Radiowelle der Frequenz ν kommt in Resonanz mit den Ionosphärenelektronen. Die Folge ist ein eigenartiges Dispersions- und Absorptionsverhalten. Die Radiowelle wird in einem großen Bereich des Einfallwinkels total reflektiert - genau in der Resonanz ν_p, also bei ν = ν_p sogar bei senkrechtem Einfall, was die "Echoauslotung" der Ionosphäre ermöglicht. Längstwellen und Kurzwellen (5 bis 30 km bzw. 10 bis 20 m) erhalten so ihre enorme Reichweite, die Längstwellen durch einen Hohlleitereffekt, die Kurzwellen durch Vielfachreflexion an der Ionosphäre. Lang- und Mittelwellen (200 m bis 5000 m) hingegen werden stark absorbiert und durch Interferenzen zwischen direkten und indirekten Wellen (fading) verzerrt. Nur Wellen oberhalb einer Maximalfrequenz ν_m, die durch die Langmuir-Frequenz eines Plasmas ν_m ∼ √n_e gegeben ist und für die Ionosphäre bei einigen MHz liegt, dringen glatt durch die Ionosphäre (also UKW-, Fernseh- und Radarwellen usw.), was einerseits die Kommunikation mit Raumfahrzeugen gestattet, andererseits aber die Reichweite eines UKW- oder Fernsehsenders auf den "optischen Horizont" beschränkt.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
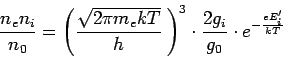