Das Volumen V ist eine Zustandsfunktion, V = nRT/p,
seine Änderung ist deshalb unabhängig, ob man erst die Temperatur
und dann den Druck ändert oder umgekehrt, d.h. die Zustandsänderung
ist unabhängig vom Weg. Mathematisch bedeutet dies, dass wir
die (infinitesimale) Änderung einer Zustandsgröße als totales
Differential schreiben können. Wegen der grundlegenden Bedeutung
dieser Aussage wollen wir uns in allgemeiner Form näher damit beschäftigen.
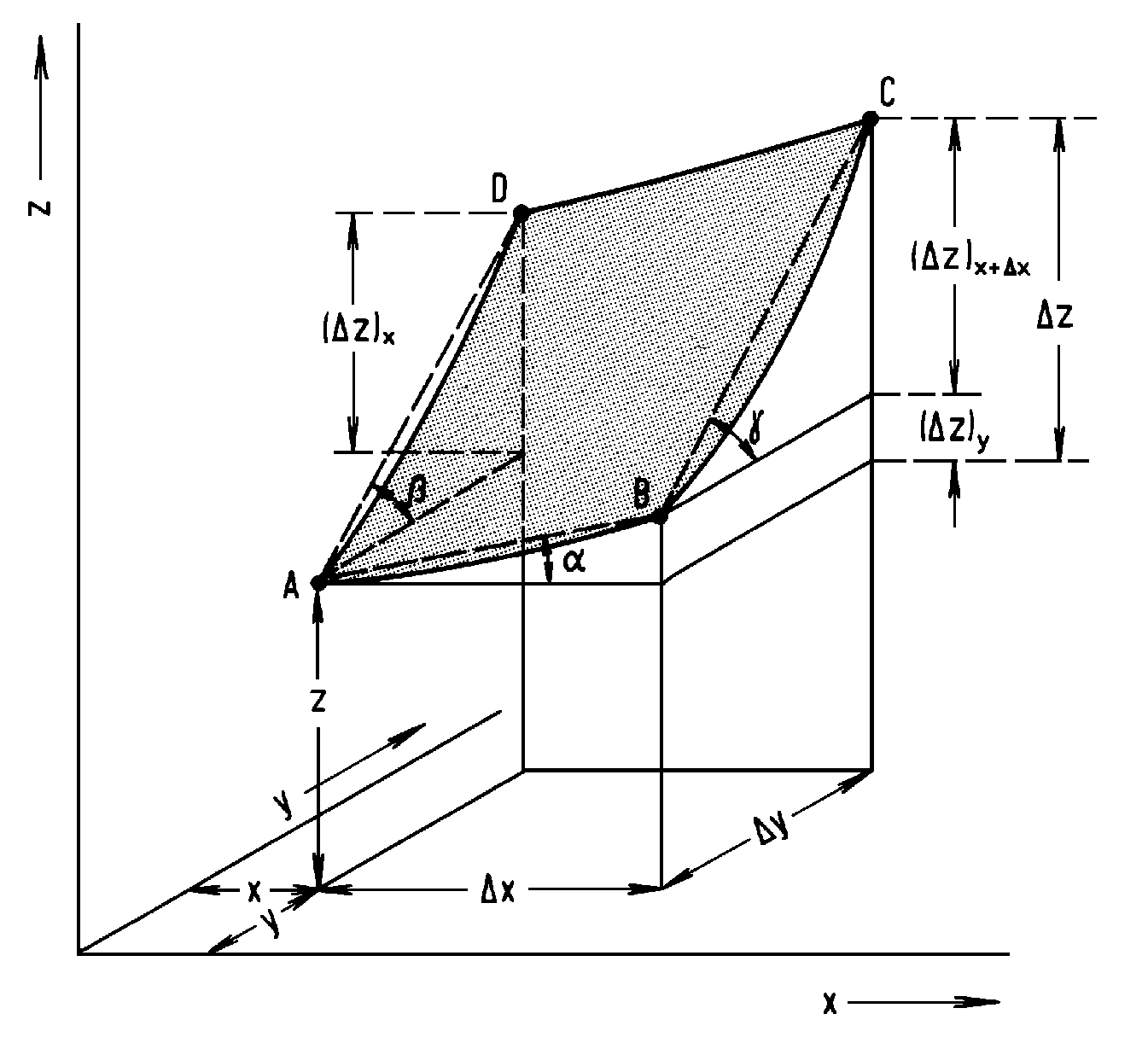 |
| Abb. 1: Zur Ableitung des totalen Differentials |
In der Abbildung stellt die graue Fläche einen Teil der Gesamtfläche z = f(x, y) dar. Wir wollen nun danach fragen, um welchen Betrag dz sich die Funktion z = f(x, y) ändert, wenn sich die beiden unabhängigen Variablen x und y um kleine Beträge dx und dy ändern. Wir betrachten zunächst eine endliche Änderung Δz, die wir beim Übergang vom Punkt A zum Punkt C feststellen. Zweckmäßigerweise halten wir zunächst die y-Koordinate fest und gelangen vom Punkt A zum Punkt B. Der Höhenzuwachs (Δz)y ergibt sich einfach als Δx tg α. Nun gehen wir bei festgehaltener x-Koordinate (x + Δx) zum Punkt C und stellen einen weiteren Höhenzuwachs (Δz)x + Δx fest, der sich zu Δy tg γ ergibt. Es gilt also für den gesamten Höhenzuwachs
Lassen wir jetzt die Punkte A bis D nahe aneinander herankommen, betrachten
also nicht mehr endliche, sondern differentielle Änderungen dx und
dy, dann werden die Sekanten AB und BC mit den Tangenten an die Fläche
z = f(x, y) im Punkt A in x- bzw. y-Richtung identisch. Insbesondere
wird dann auch der Winkel γ gleich dem Winkel
β:
| dz = (∂z/∂x)y dx + (∂z/∂y)xdy |
Die Differentialquotienten (∂z/∂x)y und (∂z/∂y)x schreiben wir mit runden ∂ und nennen sie partielle Differentialquotienten, wobei die als Index aufgeführte Variable festgehalten wurde.
Diese Gleichung nennt man totales Differential. Aus der Herleitung ergibt sich unmittelbar, dass wir dz nur dann als totales Differential schreiben können, wenn z eine eindeutige Funktion von x und y ist, d.h. wenn die Änderung von z unabhängig vom Weg ist, auf dem wir sie erreichen. Dann sind auch die partiellen Differentialquotienten stetige Funktionen von x und y und es existiert in dem betrachteten Punkt eine Tangentialebene an die Fläche.
In ganz entsprechender Weise, wie wir es hier für eine Funktion von zwei Veränderlichen durchgeführt haben, kann man auch die totalen Differentiale von Funktionen mehrerer Veränderlicher ausdrücken, z.B. für z = f(v,w,x,y)
du = (∂u/∂v)w,x,y dv + (∂u/∂w)v,x,ydw + (∂u/∂x)v,w,y dx + (∂u/∂y)v,w,x dy .
Wir können noch einige wichtige Beziehungen zwischen den partiellen Differentialquotienten herleiten, wenn wir dz = 0 setzen (in der Gl. im obigen Kasten). Es ist dann wegen
0 = (∂z/∂x)y dx + (∂z/∂y)xdy
| (∂x/∂y)z·(∂z/∂x)y = - (∂z/∂y)x |
Die Änderung des molaren Volumens Vm(T, p) können wir als totales Differential schreiben
dVm = (∂Vm/∂T)pdT + (∂Vm/∂p)Tdp.
Die erste partielle Ableitung gibt
an, wie sich das Volumen mit der Temperatur ändert; die zweite partielle
Ableitung charakterisiert die Änderung des Volumens mit dem Druck.
Wir wollen nun den thermischen Ausdehnungskoeffizienten α
durch
| α = 1/V(∂V/∂T)p |
und die Kompressibilität
χ durch
| χ = -1/V(∂V/∂p)T |
dVm/Vm = α dT -χdp = dV/V
schreiben. Bei kleinen Temperatur- und Druckänderungen (ΔT,
Δp) ist die prozentuale Volumenänderung ΔV/V
= αΔT - χΔp.
Führen wir noch den Spannungskoeffizienten β
| β = 1/p ·(∂p/∂T)V |
ein, dann folgt daraus
|
|
Diese Beziehung zwischen dem thermischen Ausdehnungskoeffizienten, dem Spannungskoeffizienten und dem Kompressibilitätskoeffizienten gilt ganz allgemein, da bei der Herleitung keinerlei spezielle Annahmen (z.B. ideales Gas) gemacht wurden.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.