Die Van-der-Waalssche Gleichung


Die von Johannes van der Waals 1873 vorgeschlagene Zustandsgleichung ist ein gutes Beispiel für sinnvolle, auf den physikalischen Inhalt gerichtete Vereinfachung eines komplizierten mathematischen Problems. Van der Waals leitete sie auf der Grundlage experimenteller Ergebnisse und exakter thermodynamischer Zusammenhänge ab.

Der Aufbau der Gleichung
Die Abstoßung zwischen den Molekülen wird berücksichtigt, indem man die Teilchen als kleine harte Kugeln auffasst. Durch das von Null verschiedene Eigenvolumen der Moleküle können diese sich nicht im Gesamtvolumen V, sondern nur im Volumenanteil (V - nb) bewegen (nb entspricht etwa der Summe der Eigenvolumina). Dies führt zum Ersatz der Zustandsgleichung des idealen Gases, pV = nRT, durch

Der durch ein Gas auf die Gefäßwand ausgeübte Druck resultiert aus Stößen zwischen Gasteilchen und Wand. Durch zwischenmolekulare Anziehungskräfte reduzieren sich sowohl die Häufigkeit von Stößen als auch die dabei wirkenden Kräfte, und zwar in beiden Fällen proportional. Somit ist die Druckverminderung aufgrund solcher Anziehungskräfte proportional dem Quadrat der Konzentration und wird im Term a(n/V)2 gefasst, wobei a eine stoffspezifische positive Konstante ist. Über die angestellten Betrachtungen gelangt man zur van-der-Waalsschen Gleichung

Van-der-Waals- Koeffizienten einiger Gase
Gas 
a 
 b 
atm dm6/mol2  dm3/mol 
 ideal   0.0   0.0
 He   0.034  0.0237
 Ar   1.345   0.0322
 O2  1.360   0.0318
 N2  1.390  0.0391
 CO2  3.592  0.0427
 CH4  2.253  0.0428
 H2  0.244  0.0266

Gewöhnlich schreibt man sie als Funktion des molaren Volumens Vm = V/n:

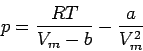
Wir wollen untersuchen, inwieweit das Verhalten realer Gase durch die Van-der Waalssche Gleichung adäquat wiedergegeben wird. Der Anspruch, mit einer einzigen, einfachen Gleichung alle möglichen Zustände aller Stoffe erfassen zu können, ist viel zu hoch. Der Vorteil der Van-der-Waalsschen Gleichung  liegt darin, dass sie eine analytische Form hat und sich zum Ableiten einiger genereller Eigenschaften realer Gase eignet. Wenn diese Gleichung versagt, kann man eine andere Zustandsgleichung verwenden oder kommt zur Virialgleichung zurück.

Die van-der Waalssche Gleichung und die Verflüssigung von Gasen
Die van-der-Waalssche Gleichung gibt das pVT-Verhalten von Gasen, die nicht zu weit von der Idealität abweichen, recht genau wieder. Wenden wir die Gleichung auf Gase in Zuständen an, die stark von der Idealität abweichen, erhalten wir zwar keine quantitative Wiedergabe der Verhältnisse mehr, immerhin jedoch noch ein interessantes qualitatives Bild. Ein typisches Beispiel zeigt die Abbildung, in der die Van-der-Waalsschen Isothermen  (gestrichelte Linien) mit den experimentellen Isothermen für Kohlendioxid verglichen werden.

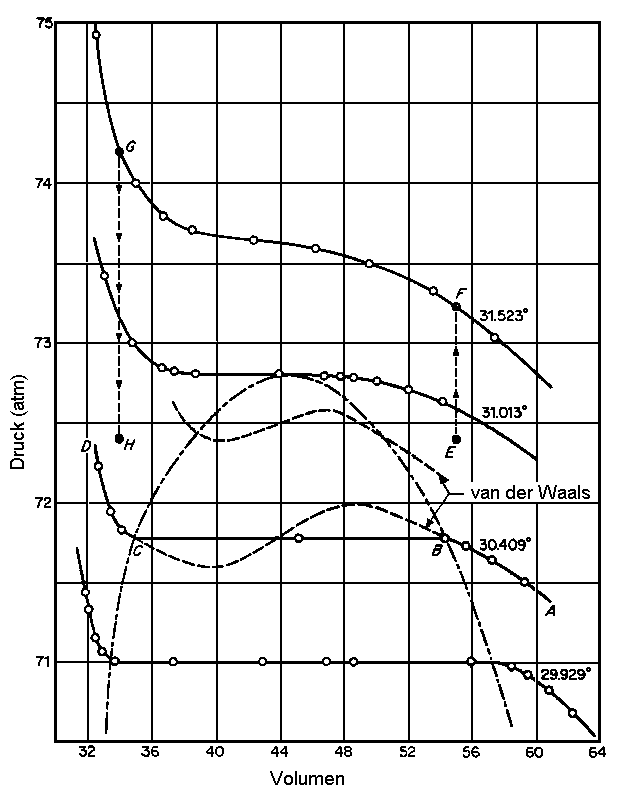Abb. 1: Isothermen des CO2 im kritischen Bereich.
Wie man sieht, gibt die Van-der-Waalssche Gleichung die Isothermen für den homogenen Dampf und selbst für die homogene Flüssigkeit noch recht genau an. Erwartungsgemäß kann die Gleichung die Diskontinuität während der Verflüssigung nicht beschreiben. Statt der experimentell bestimmten geraden Linie zeigen die van-der-Waalsschen Kurven ein Maximum und ein Minimum innerhalb des Bereichs der zwei koexistenten Phasen, die sich bei Annäherung der Temperatur an den kritischen Wert einander nähern. Beim kritischen Punkt selbst sind sie identisch geworden und bilden nun einen Sattelpunkt in der pV-Kurve. Die mathematische Bedingung für ein Maximum ist, dass (dp/dV)T = 0 und (d2p/dV2)T < 0 ist; für ein Minimum wird verlangt, dass (dp/dV)T = 0 und (d2p/dV2)T > 0 ist.


An einem Sattelpunkt nehmen sowohl die erste als auch die zweite Ableitung den Wert Null an. Also müssen am kritischen Punkt für ein Mol eines Gases die folgenden drei Gleichungen erfüllt sein (mit T = Tc, V = Vc, p = pc, n = 1):

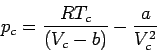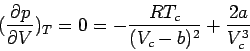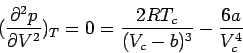Bei der Auflösung dieser Gleichung für die kritischen Größen erhalten wir:

Wenn wir diese Ausdrücke nutzen, um reduzierte Zustandsvariablen pr, Vr und Tr in das Gleichungssystem einzusetzen, dann erhalten wir:

Die Van-der-Waalssche Gleichung erhält dann die folgende einfache Form:

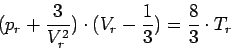Unterhalb der kritischen Temperatur treten so genannte Van-der-Waals-Schleifen auf, die nicht das reale Verhalten wiedergeben, denn ihnen zufolge müsste in einem bestimmten Bereich eine Druckerhöhung zu einer Volumenvergrößerung führen. Sie wurden deshalb so durch horizontale Linien ersetzt, dass sich zwischen Kurve und Linie oberhalb und unterhalb der Verbindung gleiche Flächen ergeben, eine Methode, die von Maxwell eingeführt wurde. Durch Anpassung der berechneten Kurve an die experimentellen Daten mittels Regressionsrechnung erhält man die van-der-Waals-Koeffizienten.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.