Die Enthalpie

Wenn das Volumen des Systems nicht konstant gehalten wird, ist die Änderung der Inneren Energie nicht mehr gleich der zugeführten Wärmemenge. Unter diesen Bedingungen wird ein Teil dieser Energie als Volumenarbeit mit der Umgebung ausgetauscht (siehe Abbildung), so dass dU < dq ist.

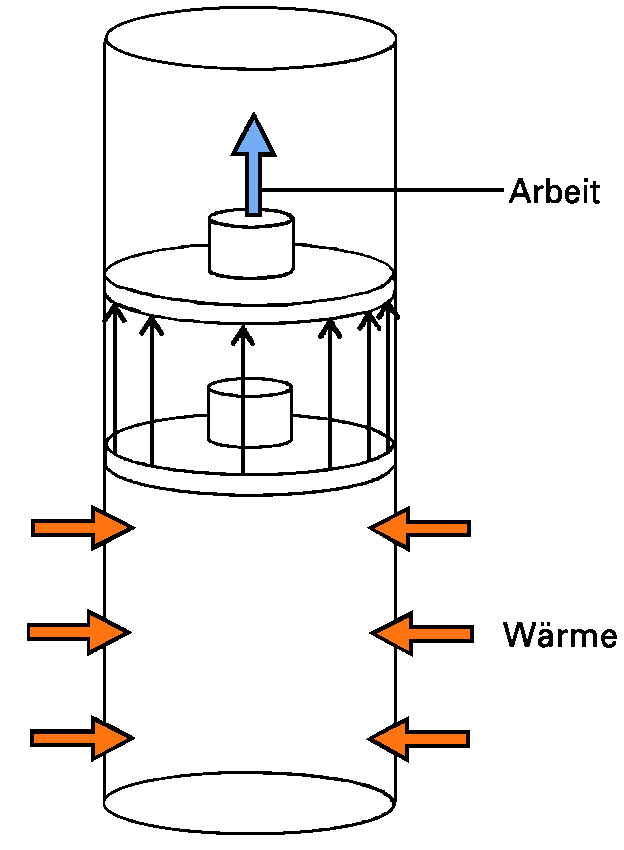Abb. 1: Wenn ein System bei konstantem Druck sein Volumen ungehindert ändern kann, kann bei Zufuhr einer Wärmemenge ein Teil davon in Form von Arbeit wieder an die Umgebung abgegeben werden. Dadurch ist in diesem Fall die Änderung der Inneren Energie geringer als die zugeführte Wärmemenge.

Da sehr viele Reaktionen, sei es im chemischen Experiment oder auch im Organismus eines Lebewesens, bei konstantem Druck (und nicht bei konstantem Volumen) ablaufen, ist es äußerst zweckmäßig, eine neue Größe zu definieren, deren Änderung gleich der zugeführten Wärmemenge dq bei konstantem Druck ist. Wir nennen diese Größe die Enthalpie H, für die gilt : dH = dq_p (konstanter Druck, nur Volumenarbeit). Wir werden zeigen, dass die Definition der Enthalpie

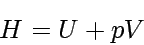mit p als Druck und V als Volumen des Systems die Gleichung dH = dq erfüllt. (Der Term pV tritt in der Definition von H für alle Systeme auf; dass in der Zustandsgleichung des idealen Gases auch pV vorkommt, ist nur ein Zufall.) Da sowohl U als auch p und V nur vom aktuellen Zustand des Systems abhängen, ist auch die Enthalpie eine Zustandsfunktion. Wie für jede Zustandsfunktion gilt auch hier, dass die Änderung der Enthalpie während eines Prozesses nur vom Ausgangs- und Endzustand des Systems, nicht aber vom Weg zwischen den beiden abhängt.

Für eine infinitesimale Zustandsänderung der Enthalpie erhalten wir: dH = dU + Vdp + pdV. Mit dU = dq - pdV wird daraus

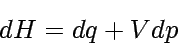Für konstanten Druck, dp = 0, folgt damit

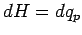
Wenn ein System bei konstantem Druck gehalten wird und nur Volumenarbeit verrichten kann, ist die Enthalpieänderung gleich der zugeführten Wärmemenge. Wenn man beispielsweise einer Heizspirale in einem mit Wasser gefüllten Becherglas eine elektrische Energie von 36 kJ zuführt, wächst dadurch die Enthalpie des Wassers um die 36 kJ; wir schreiben ΔH = +36 kJ.
 

Die Messung der Enthalpieänderung

Die Änderung der Enthalpie während einer physikalischen oder chemischen Umwandlung bei konstantem Druck kann man kalorimetrisch aus der Änderung der Temperatur des Systems bestimmen. Für Verbrennungsreaktionen kommt beispielsweise das adiabatische Verbrennungskalorimeter zur Anwendung. Die Substanz wird eingewogen, in einer Sauerstoffatmosphäre verbrannt und die Temperaturänderung ΔT wird gemessen. Ein anderer Weg zu ΔH führt über die Messung der Änderung der Inneren Energie in einem Bombenkalorimeter mit anschließender Umrechnung von ΔU in ΔH. Da Flüssigkeiten und Feststoffe (im Vergleich zu Gasen) kleine molare Volumina haben, wird auch das Produkt pV_m hier so klein, dass man molare Enthalpie und molare Innere Energie näherungsweise gleichsetzen darf. Wenn folglich nur Flüssigkeiten und Feststoffe am Prozeß beteiligt sind, setzt man auch die Änderung dieser Größen - also ΔU und ΔH - in guter Näherung gleich. Physikalisch beobachtet man bei solchen Vorgängen auch nur sehr kleine Volumenänderungen - das System verrichtet praktisch keine Volumenarbeit, sämtliche zugeführte Energie wird in Wärmeeffekte umgesetzt.

Die Beziehung zwischen Innerer Energie und Enthalpie eines idealen Gases erhalten wir durch Einsetzen der Zustandsgleichung des idealen Gases in die Definition von H,

Daraus folgt, dass sich die Änderung der Enthalpie in einer Reaktion, bei der gasförmige Stoffe entstehen oder verbraucht werden, über

ΔH  =  ΔU+ Δn_gRT

(für T=konstant) berechnet werden kann, mit Δn_g als Änderung der Stoffmenge der an der Raktion beteiligten Gase. Betrachten wir beispielsweise die Knallgasreaktion:

2H₂(g) + O₂(g) → 2H₂O(l),        Δn_g  =  -3mol

bei der 3 mol gasförmiger Stoffe zu 2 mol Flüssigkeit umgesetzt werden, deren Volumen relativ zum Gasvolumen vernachlässigbar ist. Bei 298 K ist der Zusammenhang zwischen Änderung von Enthalpie und Innerer Energie während dieses Prozesses

ΔH  - ΔU  = Δn_gRT =  - 3mol · RT  ≈ - 7,5 kJ.

Wenn die Temperatur eines Stoffes steigt, nimmt auch seine Enthalpie zu. Beim Auftragen der Enthalpie gegen sie Temperatur erhöht man dann eine Kurve (nahezu eine Gerade), deren Steigung als Wärmekapazität bei konstantem Druck, C_p, bezeichnet wird.

Die Wärmekapazität bei konstanten Druck

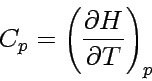ist in Analogie zur Wärmekapazität bei konstantem Volumen definiert; beides sind extensive Eigenschaften. Die entsprechende intensive Eigenschaft ist die molare Wärmekapazität bei konstanten Druck, C_p,m, definiert als Wärmekapazität pro Mol eines Stoffes: C_p,m  =  ^Cp/_n.

Mit Hilfe der Wärmekapazität bei konstantem Druck kann man eine Beziehung zwischen Enthalpieänderung und Temperaturänderung herstellen. Für infinitesimale Temperaturänderungen gilt

Wenn die Wärmekapazität über einen bestimmten Temperaturbereich hinreichend konstant ist, kann man für endliche Änderungen in diesem Bereich auch schreiben

ΔH  =  C_pΔT          (bei konstantem Druck)

Eine Erhöhung der Enthalpie kann stets einer Zuführung einer Wärmemenge bei konstantem Druck gleichgesetzt werden; in der Praxis verwendet man die Gleichung daher in der Form

Δq_p  =  C_pΔT.

Aus dieser Gleichung können wir auch ablesen, wie die Wärmekapazität eines Stoffes gemessen werden kann: Eine bestimmte Wärmemenge Δq_p wird der Substanz bei konstantem Druck zugeführt (letztere Bedingung ist immer erfüllt, wenn das Experiment in einem offenem Gefäß abläuft), dabei wird die Temperaturänderung ΔT verfolgt.

In engen Temperaturbereichen darf man die Temperaturabhängigkeit der Wärmekapazität näherungsweise ignorieren; für ein einatomiges ideales Gas (etwa ein Edelgas) stellt dies eine recht genaue Näherung dar. Für die Fälle, bei denen eine Vernachlässigung dieser Abhängigkeit nicht sinnvoll ist, hat sich die empirische Näherungsfunktion

C_p,m  =  a + bT +  c/T²

als zweckmäßig erwiesen.
 
 

Temperaturabhängigkeit der molaren Wärmekapazität, Cp,m  / JK-1mol-1 = a + bT + c/T2
	a	b / (10-3 K-1)	c / (105 K2)
C (s, Graphit)	16,86	4,77	-8,54
CO2 (g)	44,22	8,79	-8,62
H2O (l)	75,29	0	0
N2 (g)	28,58	3,77	-0,50

Der Zusammenhang zwischen C_V und C_p

Die meisten Substanzen dehnen sich aus, wenn sie bei konstantem Druck erwärmt werden. Dabei verrichten sie Arbeit an der Umgebung und geben einen Teil der als Wärme zugeführten Energie wieder nach außen ab. Ihre Temperatur nimmt auf diese Weise weniger zu, als wenn das Volumen des Systems während der Erwärmung konstant gehalten würde. Ein geringerer Temperaturanstieg weist auf eine größere Wärmekapazität hin; wir können schließen, dass in den meisten Fällen die Wärmekapazität eines Stoffes bei konstantem Druck größer ist als die Wärmekapazität bei konstantem Volumen. Es gilt

.

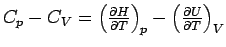In diesen Ausdruck setzen wir für ideale Gase

H  =  U + pV  = U + nRT

ein und erhalten

C_p - C_V =  (^∂U/_∂T)_p + nR - (^∂U/_∂T)_V.

Da für ideale Gase (^∂U/_∂T)_p  =  (^∂U/_∂T)_V  gilt die einfache Beziehung:

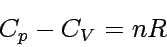Daraus folgt, dass die molare Wärmekapazität eines idealen Gases bei konstantem Druck um etwa 8 J K^-1mol^-1 größer ist als bei konstantem Volumen. Wenn wir bedenken, dass die molare Wärmekapazität eines einatomigen Gases bei konstantem Volumen etwa 25 J K^-1mol^-1 beträgt, wird klar, dass diese Differenz keinesfalls vernachlässigt werden kann. Man kann ganz allgemein zeigen, dass für alle Stoffe die universelle thermodynamische Beziehung gilt:

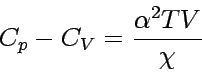Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.