Wärme

Dem unbefangenen Betrachter drängt sich die Auffassung geradezu auf, dass ein wärmerer Körper während seiner Abkühlung "etwas" abgibt, was der kühlere Körper während der Erwärmung aufnimmt. Dieses "Etwas" bezeichnen wir, um einen prägenden Namen dafür zu haben, nach Black als Wärmemenge. In dieser Ausdrucksweise gibt der Körper mit der höheren Temperatur an den mit der tieferen eine Wärmemenge ab. Der Verlust der Wärmemenge wird als die Ursache der Abkühlung des einen Körpers, ihre Aufnahme durch den anderen Körper als die Ursache seiner Erwärmung betrachtet. Dieser neu eingeführte "Quantitätsbegriff" der Wärme, der dem "Intensitätsbegriff" Temperatur zur Seite treten soll, gewinnt erst dadurch eine wirkliche Bedeutung, dass wir die "Wärmemenge" messen und zahlenmäßig angeben können.

Eine Messung der Wärmemenge kann auch hier wieder nur durch die Messung ihrer Wirkungen geschehen, und von solchen Wirkungen kennen wir vorläufig nur die Temperaturänderungen. Wir werden also die von einem Körper aufgenommene (oder abgegebene) Wärmemenge Δq dessen Temperaturänderung ΔT vor und nach der Aufnahme (oder Abgabe) proportional setzen: Δq  ~ ΔT; oder mit der Proportionalitätskonstanten C:

Δq = C ·ΔT,

Δq  =  c · m  · ΔT

Da es sich hier immer um Temperaturdifferenzen handelt, gilt die Gleichung ebenso für die Celsiustemperatur t. In dieser Gleichung erweist sich c als ein vom Material abhängiger Faktor. Sie enthält aber zwei Unbekannte, nämlich Δq und c. Würden wir die spezifische Wärmekapazität c kennen oder zu messen verstehen, so könnten wir auch die Wärmemenge Δq  messen und umgekehrt.

Früher legte man für eine beliebige Substanz in einem bestimmten Temperaturintervall den Faktor c willkürlich fest. Es wurde vereinbart, dass Wasser zwischen 14,5 und 15,5 °C die Einheit der spezifischen Wärmekapazität haben soll. Mit dieser Festsetzung war gleichzeitig die Einheit der Wärmemenge definiert und damit die Möglichkeit gewonnen, beliebige Wärmemengen zu messen. Die Einheit der Wärmemenge ergibt sich dann so: Setzt man c gleich der Einheit und m = 1 g, indem man 1 g Wasser von 14,5 °C unter Normaldruck auf 15,5 °C erwärmt, so dass die Temperaturdifferenz Δt = 1 Grad ist, so wird Δq gleich der Einheit der Wärmemenge. Man nannte sie 1 Kalorie (1 cal).

Die Masse steht hier stellvertretend für die Stoffmenge. Oft ist es aber zweckmäßig, die Wärmekapazität unmittelbar auf die Stoffmenge zu beziehen. Man spricht dann von der molaren Wärmekapazität C_m. Zwischen C_m und c besteht der Zusammenhang

C_m = M · c

wobei M die molare Masse ist. Bei der geschilderten Festsetzung der Einheit der Wärmemenge ist man an die Stoffeigenschaften des Wassers gebunden. Es besteht jedoch die Tendenz, bei der Definition von Einheiten so weit wie möglich ohne Stoffeigenschaften auszukommen.

Was ist dann aber die wahre Natur der Wärme? Da sie z.B. durch Reibung, d.h. durch Arbeit erzeugt werden kann, liegt der Gedanke nahe, dass sie eine Form der Energie sei. Wenn dies der Fall ist, muss man erwarten, dass eine bestimmte Arbeit, wenn sie in Wärme umgewandelt wird, jedesmal eine ganz bestimmte Wärmemenge erzeugt, und zwar unabhängig davon, auf welche Weise die Umwandlung von Arbeit in Wärme vor sich geht, d.h. unabhängig von der Art des verwendeten Prozesses wie auch von den physikalischen und chemischen Eigenschaften der benutzten Stoffe. Mit anderen Worten: Zwischen der früher in Kalorien gemessenen Wärme und der zu ihrer Erzeugung aufgewendeten Arbeit, die in Joule gemessen wird, muss ein festes Zahlenverhältnis bestehen.

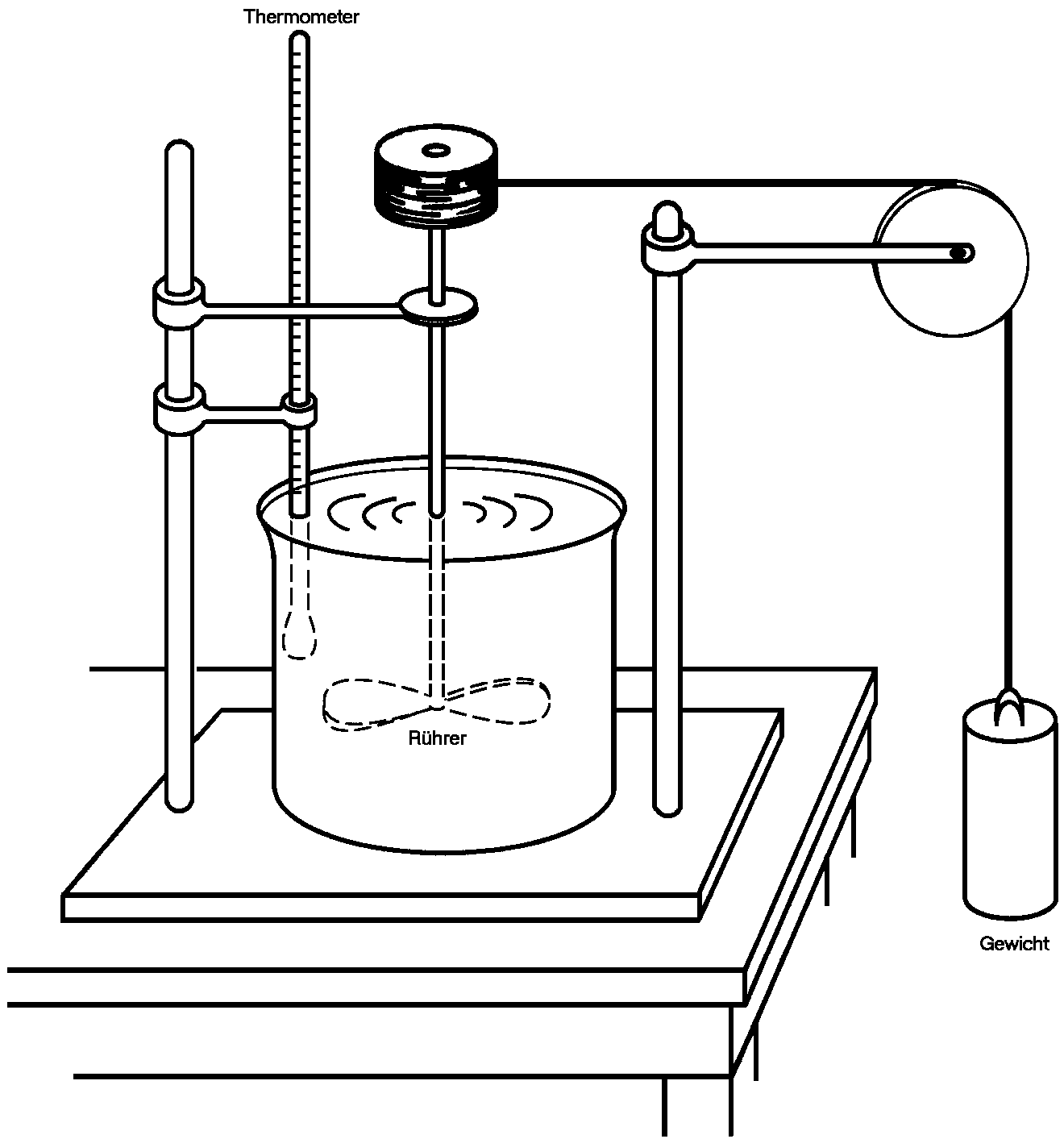Abb. 1: Joules Apparatur zur Bestimmung des mechanischen Wärmeäquivalents. Das sich herabsenkende Gewicht leistet Arbeit, E = mgh, im Wasser des Behälters, wobei die Energie E über die Temperaturveränderung bestimmt werden kann.

J.P. Joule hat in den Jahren 1842 bis 1850 durch systematische Versuche diesen Nachweis erbracht. Der Gedankengang eines seiner Experimente ist folgender: Ein Körper der Masse m, der auf die Höhe h gehoben ist, besitzt eine potentielle Energie mgh. Wenn dieser Körper sinkt, so leistet er Arbeit, und diese wird in folgender Weise in Wäme umgesetzt: Der sinkende Körper bewegt ein Schaufelrad, das sich unter starker Reibung in einer Flüssigkeit (z.B. Quecksilber) dreht. Ist der Körper M herabgesunken, so ist die Energie mgh verschwunden, aber dafür Wärme in der Flüssigkeit aufgetreten. Ist deren Masse m, ihre spezifische Wärmekapazität c, ihre Temperaturerhöhung ΔT, so ist die erzeugte Wärmemenge gleich mcΔT. Nun muss der Quotient ^mgh/_mcΔT, wenn die Wärme eine Energieform ist, konstant und unabhängig von den Versuchsbedingungen sein. Heute gilt:

1 Kalorie (cal)  = 4.1868 Joule (J)

Wenn man nicht oft mit diesen Zahlen zu rechnen hat, hat man kaum ein "Gefühl" dafür, wieviel eine Kalorie, ein Newtonmeter oder ein Joule ist. Am leichtesten kann man noch aus dem Verbrauch elektrischer Energie eine Kilowattstunde abschätzen. Es ist lohnend und überraschend, einfache Vergleiche zu ziehen, entweder durch Rechnungen oder durch einfache Messungen. So ergibt sich für die kinetische Energie einer Pistolenkugel ein Betrag von 100 J. Dagegen gibt ein Streichholz eine Wärmeenergie von 1000 J ab.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.