Der CARNOTsche Kreisprozess zeigt uns die Wirkungsweise einer idealisierten Maschine, in der Wärme aus einem Wärmebehälter der Temperatur Tw teilweise in Arbeit verwandelt und zum anderen Teil an einen kälteren Behälter der Temperatur Tk abgegeben wird.
| Wärmebehälter bei Tw | ||
| ↓ qw | ||
| w3 → w4 → |
Maschine | → − w1 → − w2 |
| ↓ − qk | ||
| Wärmebehälter bei Tk |
Der Stoff, der die Wärme transportiert und die Arbeit verrichtet, wird zum Schluss in denselben Zustand zurückgebracht, den er ursprünglich besaß; einen solchen Vorgang nennt man Kreisprozess.
Die in dem Zyklus auftretenden Reaktionsschritte werden reversibel durchgeführt.
Um den Vorgang möglichst eindeutig zu machen, wählen wir als
arbeitenden Stoff ein Gas, das nicht ideal zu sein braucht. Bei Setzen
der Vorzeichen gehen wir dabei vom arbeitenden Gas der Maschine als System
aus. Wenn wir nun die Maschine einen Zyklus lang betreiben, dann erhalten
wir die folgenden Einzelschritte:
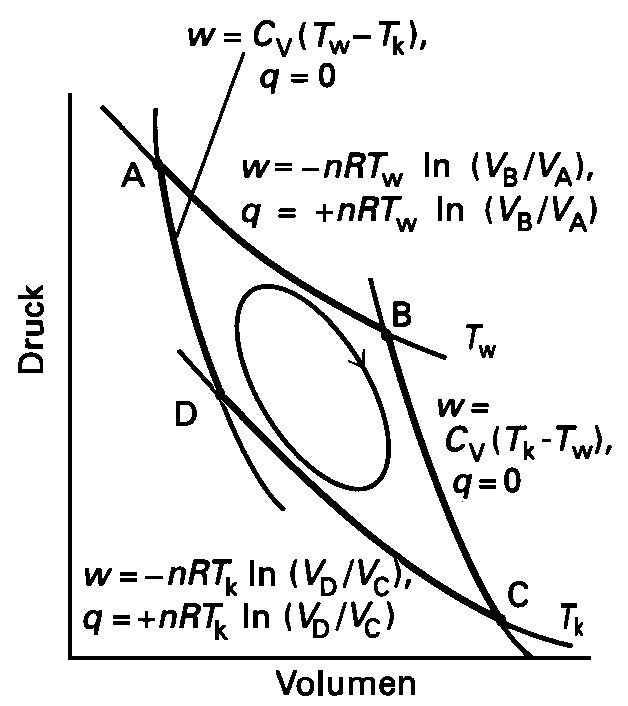 |
| Abb. 1: Carnotscher Kreisprozess für ein ideales Gas. Alle Schritte sind thermodynamisch reversibel. Von A nach B führt eine isotherme Expansion bei der Temperatur Tw, von B nach C eine adiabatische Expansion mit Verringerung der Temperatur auf Tk. Von C nach D verläuft eine isotherme Kompression bei Tk, der Kreis wird geschlossen durch eine adiabatische Kompression von D nach A. Die Temperatur beträgt dann wieder Tw. Dargestellt sind die aufgenommene Wärme und die verrichtete Arbeit für jeden Teilschritt. |
(1) Isotherme - reversible Expansion des Gases von VA auf VB. Hierbei entzieht das Gas dem Wärmebehälter bei der Temperatur Tw die Wärmemenge qw. Gleichzeitig verrichtet das Gas Arbeit an seiner Umgebung. [für ideales Gas: w1 = -nRTw ln(VB/VA), qw = -w1]
(2) Adiabatisch-reversible Expansion von VB auf VC. Hierbei findet kein Wärmeaustausch statt (q = 0). Das Gas verrichtet Arbeit und kühlt sich von Tw auf Tk ab. [für ideales Gas: w2 = CV (Tk - Tw), q = 0]
(3) Isotherm-reversible Kompression des Gases von VC auf VD bei der Temperatur Tk. Hierbei wird am Gas die Arbeit w3 verrichtet; gleichzeitig gibt das Gas die Wärmemenge -qk bei der Temperatur Tk an den kälteren Wärmebehälter ab. [w3 = -nRTk ln(VD/VC), qk = -w3]
(4) Adiabatisch-reversible Kompression des Gases von VD auf VA. Hierbei wird am Gas die Arbeit w4 verrichtet; da kein Wärmeaustausch stattfindet (q = 0), erwärmt sich das Gas von Tk auf Tw. [ideales Gas: w4 = CV (Tw - Tk), q = 0]
Der I. Hauptsatz der Thermodynamik fordert nun, dass für einen solchen Kreisprozess ΔU = 0 ist. Nun ist ΔU die Summe aus allen aufgenommenen und abgegebenen Arbeitsbeträgen (w = w1 + w2 + w3 + w4) und den Wärmemengen (qw + qk)
ΔU = q + w = qw + qk + w = 0
Die von der Maschine verrichtete Arbeit ist daher gleich der dem Wärmebehälter
entnommenen Wärmemenge, verringert um die nach Arbeitsverrichtung an
den kühleren Behälter abgegebene Wärmemenge:
-w = qw - (-qk) = qw + qk.
Der Wirkungsgrad der Maschine ist demnach:
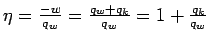
Da bei diesem Kreisprozess jeder Schritt reversibel durchgeführt wird, erhalten wir insgesamt auch die maximal mögliche Arbeit, die das System mit dem gewählten arbeitenden Stoff und in dem gewählten Temperaturbereich verrichten kann.
Den Quotienten -w/qw für den Wirkungsgrad kann man noch vereinfachen, wenn man die Beziehung zwischen der Temperatur und dem Volumen [(Tk/Tw)c = VA/VD = VB/VC] für reversibel adiabatische Prozesse berücksichtigt:
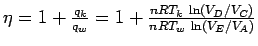
Da
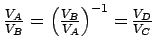
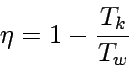 |
Die Entropie
Wir können einen reversiblen Carnotschen Kreisprozeß in den Temperaturgrenzen Tw und Tk auch folgendermaßen umschreiben:
qw/Tw + qk/Tk =
nR lnVB/VA + nR lnVD/VC
= nR lnVB/VA − nR
ln VB/VA = 0
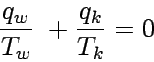 |
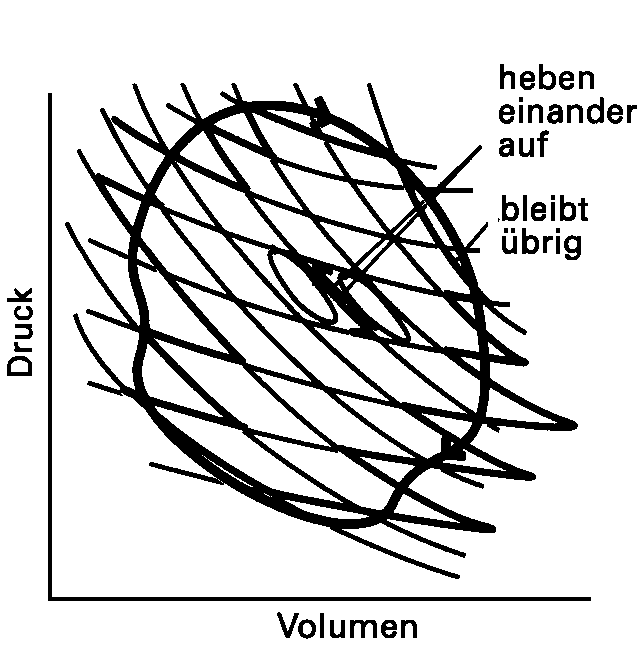 |
| Abb. 2: Ein beliebiger Kreisprozeß lässt sich in eine Anzahl von Carnot-Prozessen zerlegen. Diese Zerlegung gilt exakt im Grenzfall infinitesimal kleiner Carnot-Teilprozesse. Im Inneren des Kreises heben die verschiedenen Teilprozesse einander auf, übrig bleibt nur die Peripherie des Kreises. Da die Entropieänderung für einen vollständigen Umlauf jedes einzelnen Kreisprozesses gleich null ist, wird auch das Integral über die Entropie entlang der Peripherie zu null, d.h. die Entropie ist eine Zustandsfunktion. |
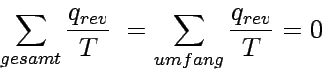
Im infinitesimalen Grenzfall fallen die übrig bleibenden Grenzen der Carnot-Prozesse genau mit dem Umfang des Gesamtprozesses zusammen, die Summe wird zum Integral:
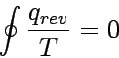
Das Verschwinden eines Kreisintegrals bedeutet, dass der Integrand ein vollständiges Differential irgendeiner Zustandsfunktion des Systems ist. Wir können daher eine neue Zustandsfunktion, die Entropie, folgendermaßen definieren:
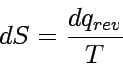 |
Für einen Übergang vom Zustand A in den Zustand B gilt:
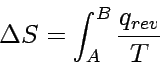 |
Die Funktion S wurde zuerst von Clausius (1865) eingeführt, die er Entropie (von "εν τρεπειν", eine Richtung geben) nannte. Die Gleichung dS = dqrev/T besagt, dass das unbestimmte Differential dqrev bei Multiplikation mit 1/T ein bestimmtes Differential wird. Der Integrand A∫Bdqrev hängt vom Reaktionsweg ab, der Integrand A∫B dqrev/T jedoch nicht. Dies ist eine weitere, alternative Aussage des II. Hauptsatzes der Thermodynamik.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.