Phasenübergänge erster und zweiter Ordnung

Es existiert eine Vielzahl unterschiedlicher Phasenübergänge. Manchen begegnet man häufig, wie zum Beispiel dem Schmelzen oder Verdampfen. Seltener sind Übergänge zwischen verschiedenen Modifikationen von Festkörpern, leitenden und supraleitenden oder flüssigen und supraflüssigen Phasen. Man kann die Übergänge anhand der thermodynamischen Eigenschaften - insbesondere anhand des chemischen Potentials - in verschiedene Klassen einordnen. Die Idee dieser Einteilung stammt von Paul Ehrenfest; man spricht auch von der Klassifikation nach Ehrenfest.

Viele gewöhnliche Phasenübergänge, wie Schmelzen und Verdampfung, verlaufen unter Änderung von Enthalpie und Volumen. Daraus ergeben sich charakteristische Merkmale für die Steigung der chemischen Potentiale der beteiligten Phasen auf beiden Seiten des Phasenübergangs. Für einen Übergang von einer Phase α zu einer Phase β gilt (wg. dµ = −S_mdT + V_mdp, bzw. dµ = V_mdp bei konstanter Temperatur oder dµ = −S_mdT bei konstantem Druck):

(dµ^β/dp)_T−(dµ^α/dp)_T = V_m^β − V_m^α = Δ_transV

(dµ^β/dT)_p−(dµ^α/dT)_p = −S_m^β− S_m^α = −Δ_transS = −Δ_transH/T.

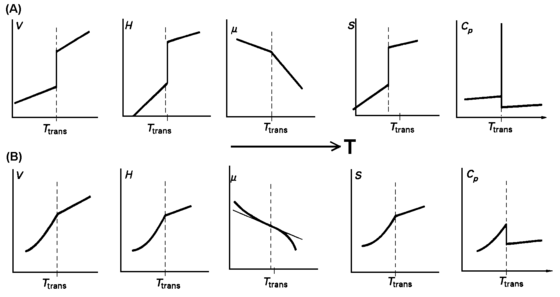Abb.1: Die Änderung der thermodynamischen Eigenschaften bei Phasenübergängen a) erster und b) zweiter Ordnung.

Sowohl ΔV als auch ΔS sind für Übergänge wie Schmelzen und Verdampfen verschieden von Null; die Steigung des chemischen Potentials als Funktion des Drucks müssen demnach auf beiden Seiten des Übergangs verschieden sein (Abb. 1a). Mit anderen Worten: Die ersten Ableitungen der chemischen Potentiale nach Druck und Temperatur ändern sich am Punkt des Phasenübergangs sprunghaft. Insbesondere nennt man einen Phasenübergang, für den die erste Ableitung des chemischen Potentials nach der Temperatur dieses Merkmal aufweist, einen Phasenübergang erster Ordnung.

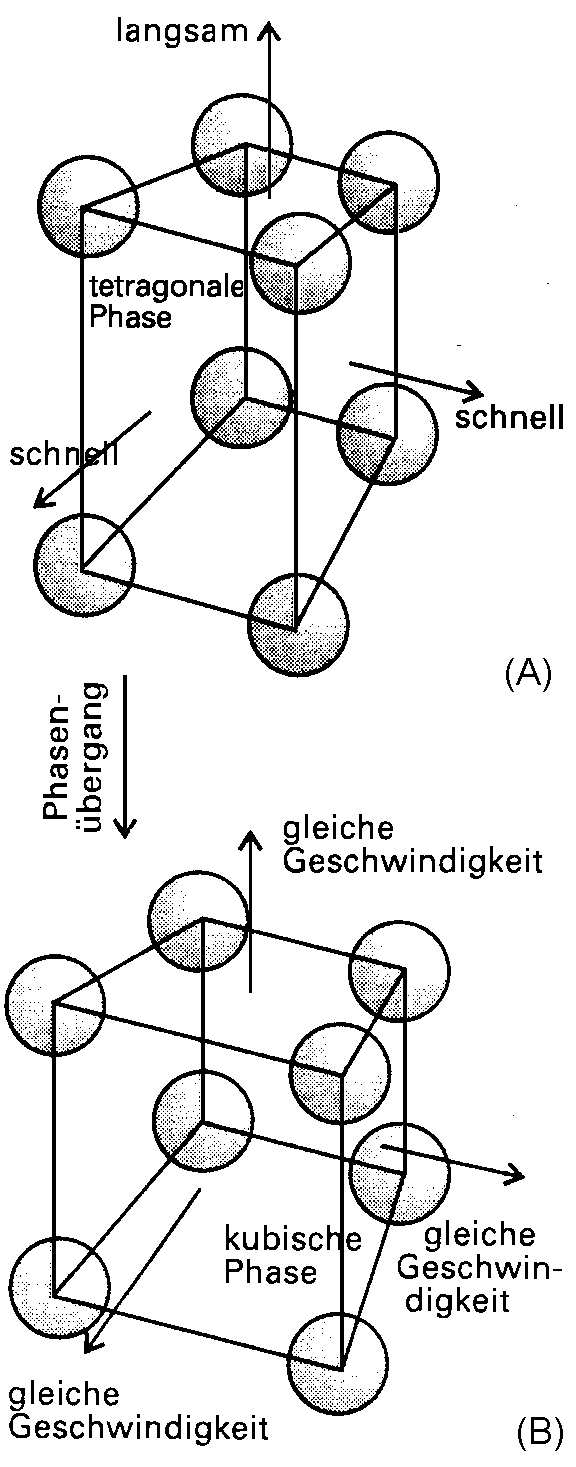Abb. 2: Ein Beispiel für einen Phasenübergang zweiter Ordnung: Die tetragonale Phase dehnt sich in zwei Raumrichtungen bevorzugt aus und wandelt sich so in eine Phase mit kubischer Symmetrie um. Die Ausdehnung erfolgt dann in allen drei nun äquivalenten Richtungen gleichmäßig. Da sich die Atome am Phasenübergangspunkt nicht sprunghaft umordnen, beobachtet man keine Übergangsenthalpie.

Die Steigung der Enthalpie als Funktion der Temperatur ist die Wärmekapazität eines Stoffes, Cp. Bei einem Übergang erster Ordnung ändert sich H bei infinitesimaler Temperaturänderung um einen endlich kleinen Betrag (siehe Abb. 1a). Am Punkt des Übergangs ist daher die Steigung von H und somit die Wärmekapazität unendlich groß (die Funktion ist an dieser Stelle singulär). Physikalisch kann man diesen Befund erklären, wenn man sich vor Augen führt, dass die Wärmezufuhr und nicht eine Temperaturerhöhung die treibende Kraft für den Übergang darstellt: Die Temperatur von siedendem Wasser bleibt gleich, obwohl ständig Wärme zugeführt wird. Die unendlich hohe Wärmekapazität bei der Phasenübergangstemperatur notieren wir als weiteres Merkmal eines Phasenübergangs erste Ordnung.

Ein Phasenübergang zweiter Ordnung im Ehrenfestschen Sinn ist dadurch charakterisiert, dass zwar die erste Ableitung von µ nach der Temperatur am Übergangspunkt stetig verläuft, nicht aber die entsprechende zweite Ableitung. Ein stetiger Verlauf von µ(T) - graphisch gesehen eine Kurve, die auf beiden Seiten in der Umgebung des Übergangs die gleiche Summe besitzt - ist ein Zeichen dafür, dass sich weder Volumen noch Entropie (und daher auch nicht die Enthalpie) während des Übergangs ändern (Abb. 1 b und Abb. 2). Die Wärmekapazität zeigt am Übergang zwar eine Unstetigkeit, wird aber nicht singulär. Beispiel für eine Phasenübergang zweiter Ordnung ist die Umwandlung der normalleitenden in die supraleitende feste Phase von Metallen bei tiefen Temperaturen. Phasenübergänge, die nicht erster Ordnung sind, bei denen jedoch eine unendlich große Wärmekapazität erreicht wird, bezeichnet man als λ-Übergänge.

Die Wärmekapazität der betreffenden Systeme steigt bereits lange vor dem eigentlichen Phasenübergang an. Die Gestalt der Kurve erinnert an den griechischen Buchstaben λ. Beispiele sind Ordnungs-/Unordnungsübergänge in Legierungen, das Auftreten von Ferromagnetismus und der Übergang vom flüssigen zum suprafluiden Helium.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.