Phasengrenzen (Clapeyronsche Gleichung)

Bei gegebenem Druck ist immer die Phase in einem bestimmten Temperaturbereich stabil, deren chemisches Potential dort niedriger als das jeder anderen Phase ist. Die niedrigsten chemischen Potentiale findet man für Festkörper; und damit ist die feste Phase bei tiefen Temperaturen die stabilste. Da jedoch die chemischen Potentiale der einzelnen Phasen in unterschiedlicher Weise von der Temperatur abhängen, kann bei Temperaturerhöhung das chemische Potential einer anderen Phase (einer weiteren festen, einer flüssigen oder auch einer gasförmigen) unter den Wert für den Festkörper fallen. In diesem Fall findet ein Phasenübergang statt (u. Umständen extrem langsam, wenn eine kinetische Hemmung vorliegt).

Temperaturabhängigkeit der Stabilität von Phasen
Die Temperaturabhängigkeit der Freien Enthalpie eines Systems als Funktion der Entropie ist: (∂G/∂T)p = −S. Da das chemische Potential eines reinen Stoffes seiner molaren Freien Enthalpie entspricht (µ = Gm = G/n), kann man die Temperaturabhängigkeit des chemischen Potentials als Funktion der molaren Entropie schreiben:
 

(∂µ/∂T)p  =  −Sm.

 
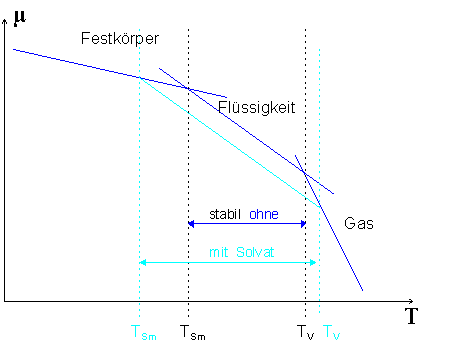Abb.1: Chemisches Potential µ für drei Phasen. Die Steigung ist durch -Sm gegeben. Mit Solvat verschiebt sich µ(l) zu niedrigeren Werten mit entsprechender Änderung des Schmelzpunktes TSm und des Siedepunktes TV. 
(Eigentlich müssten die einzelnen Geraden leicht nach unten gekrümmt sein, da die Entropie mit der Temperatur zunimmt. Zur klareren Darstellung ist aber darauf verzichtet worden.)
 Diese Beziehung drückt aus, dass das chemische Potential eines reinen Stoffes mit steigender Temperatur sinkt (da Sm immer positiv ist, ist die Steigung der Funktion µ(T) stets negativ). Da Sm(g) > Sm(l) ist, muss die Steigung der Funktion µ(T) für Gase größer als für flüssige Phasen sein. Weiterhin steigt diese Funktion fast immer für Flüssigkeiten steiler an als für Festkörper, da bis auf wenige Ausnahmen  Sm(l) > Sm(s) gilt. Die Kurve fällt für µ(l) so steil ab, dass sie bei hinreichend hoher Temperatur schließlich unterhalb von µ(s) verläuft: Die flüssige Phase wird zur stabilen, der Festkörper schmilzt. Das chemische Potential der Gasphase fällt - aufgrund seiner hohen molaren Entropie - mit steigender Temperatur stark ab; von einer bestimmten Temperatur an ist dann der gasförmige Aggregatzustand stabil, die Flüssigkeit verdampft. Um zu einem Phasenübergang zu gelangen, muss man also die chemischen Potentiale der einzelnen Phasen relativ zueinander verschieben, was man am einfachsten durch Änderung der Temperatur erreicht. Wir können uns auch qualitativ klarmachen, was geschieht, wenn wir "etwas" zu unserer reinen Substanz zugeben, z.B. Salz in Wasser lösen. Das chemische Potential der Flüssigkeit µ(l) verschiebt sich (zu kleineren Werten) und wir erwarten (s. Abb.) einen geringeren Schmelzpunkt TSm und einen höheren Siedepunkt TV. Da die Steigung von µ(s) geringer ist als die von µ(g), erwarten wir außerdem, dass die Temperaturabsenkung des Schmelzpunktes größer sein wird als die Erhöhung des Siedepunktes durch irgendwelche Verunreinigungen.
 

Die Phasengrenzlinien
Zwei Phasen, die sich miteinander im Gleichgewicht befinden, besitzen das gleiche chemische Potential. Für zwei Phasen α und β bedeutet das
 

µα(p, T)  =  µβ(p, T);

die Lösung dieser Beziehung ist die Gleichung der Phasengrenzlinie in Form einer Funktion p(T). Ein charakteristisches Merkmal  der Phasengrenzlinien ist deren Steigung dp/dT. T und p sollen sich in infinitesimalen Schritten so ändern, dass das Gleichgewicht zwischen α und β stets aufrechterhalten bleibt. Zu Beginn sind die chemischen Potentiale beider Phasen gleich (da das Gleichgewicht eingestellt ist). Wenn man sich auf die beschriebene Weise zu einem andern Punkt der Phasengrenzlinie bewegt, ist diese Beziehung immer erfüllt (da das Gleichgewicht eingestellt bleibt). Daher kann man die Änderung des chemischen Potentials beider Phasen gleichsetzen, dµα = dµβ. Wir wissen, dass für jede der beiden Phasen gilt dG = - SdT + Vdp. Division durch n ergibt:

dG/n  = dµ  = −Sm dT + Vm dp
An der Grenzlinie gilt:
−Smα dT + Vmα dp  = −Smβ dT + Vmβ dp.

Hier sind Smα und Smβ die molaren Entropien und Vmα bzw. Vmβ die molaren Volumina der jeweiligen Phase. Durch Zusammenfassen und Umformen dieser Gleichung erhalten wir

(Vmβ − Vmα) dp  =  (Smβ − Smα) dT

und daraus direkt die Clapeyronsche Gleichung
 

dp/dT  =  ΔSm/ΔVm.

Darin sind ΔSm = Smβ− Smα und ΔVm = Vmβ− Vmα die Änderungen der molaren Entropie und des molaren Volumens des Systems während des Phasenübergangs. Diese wichtige Beziehung für die Steigung der Phasengrenzlinie gilt exakt und für jedes beliebige Phasengleichgewicht eines beliebigen reinen Stoffes.
 

Die Phasengrenzlinie fest/flüssig
Der Schmelzvorgang findet bei einer Temperatur T statt und verläuft unter Änderung der molaren Enthalpie des Systems um ΔSmH. Daraus ergibt sich die molare Schmelzentropie zu ΔSmH / T; die Clapeyronsche Gleichung für diesen Vorgang lautet
 

dp/dT  =  ΔSmH/TΔSmV

ΔSmV gibt die Änderung des Molvolumens beim Schmelzen an. Die Schmelzenthalpie ist (mit Ausnahme von Helium-3) immer positiv, die Volumenänderung ist normalerweise ebenfalls positiv und stets sehr klein. Dies bedeutet, dass die Steigung dp/dT steil und im allgemeinen positiv wird. Die Funktion p(T) selbst erhält man durch Integration von dp/dT unter der Annahme, dass ΔSmH und ΔSmV nur wenig von der Temperatur abhängen und daher als Konstanten behandelt werden können. Wenn die Schmelztemperatur bei dem Druck p* gleich T* und bei dem Druck p gleich T ist, haben wir folgende Integration durchzuführen:

p*∫p dp  =  ΔSmH/ΔSmVT*∫T (dT/T).

Wir (James Thomson war der Erste) erhalten als Näherungsgleichung für die Phasengrenzlinie fest/flüssig
 

p  =  p* + ΔSmH/ΔSmV  ln (T/T*).

Für kleine Temperaturdifferenzen T - T* erhalten wir ln(T/T*) = ln(1 + (T - T*)/T*) ≈(T - T*)/T*   (wegen ln(1+x) ≈ x für kleines x):
 

p ≈  p* + ΔSmH/ΔSmV (T - T*)/T*.

Die Phasengrenzlinie flüssig/gasförmig
Die molare Verdampfungsentropie eines Stoffes bei der Temperarur T beträgt ΔVH/T; die Clapeyronsche Gleichung der Phasengrenzlinie demzufolge
 
 

dp/dT  =  ΔvH/TΔvV.

Die Verdampfungsenthalpie ist stets positiv, ΔVV ist ein großer, ebenfalls positiver Wert. Die Ableitung dp/dT ist daher auch positiv; aber wesentlich kleiner als für die Phasengrenze fest/flüssig.

Das Molvolumen eines Gases ist viel größer als das einer Flüssigkeit, so dass wir in guter Näherung ΔVV ≈ Vm(g) setzen können. Setzt man diese beiden Näherungen in die exakt gültige Clapeyronsche Gleichung ein und nimmt ferner ideales Gasverhalten (Vm(g) = RT/p) an, d.h. dp/dT  =  ΔH p/RT² , dann erhalten wir die näherungsweise gültige Clausius-Clapeyronsche-Gleichung:
 

d  ln p/dT  =  ΔVH/RT2

(Dazu haben wir dp/p = d ln p verwendet.) Wenn wir noch voraussetzen, dass die Verdampfungsenthalpie nicht von der Temperatur abhängt, können wir diese Gleichung integrieren und erhalten
 

p  =  p* exp[ΔVH/R(1/T* - 1/T)]

Hier ist p* der Dampfdruck bei der Temperatur T*, p gehört entsprechend zu T. Diese Funktion beschreibt den Verlauf der Phasengrenzlinie flüssig/gasförmig; sie endet bei der kritischen Temperatur Tkrit, da oberhalb dieser keine flüssige Phase mehr existiert.
 

Die Phasengrenzlinie fest/gasförmig
In allen für die Phasengrenze flüssig/gasförmig abgeleiteten Beziehungen tauschen wir einfach die Verdampfungsenthalpie gegen die Sublimationsenthalpie ΔSubH aus. So erhalten wir, analog zur Herleitung der Clausius-Clapeyronschen Gleichung, die folgende Beziehung für die Temperaturabhängigkeit des Sublimationsdampfdrucks:
 

d  ln p/dT ≈ ΔSubH/RT2.
p  =  p* exp[ΔSubH/R(1/T* - 1/T)]

Da die Sublimationsenthalpie ΔSubH größer als die Verdampfungsenthalpie ΔVH ist, kann man dieser Gleichung entnehmen, dass in der Nähe des Schnittpunktes beider Kurven die Sublimationsdruckkurve steiler ansteigt als die Dampfdruckkurve.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.