Ideale Gasmischungen

Das chemische Potential einer Spezies in einem idealen Gas ist

µ_i = µ_i° + RT ln p_i/p°

Für eine Mischung von (idealem) Gas ist es hilfreich den Molenbruch einzuführen:

µ_i = µ_i° + RT ln x_iP/p°

wobei die Partialdrücke p_i der Spezies i über p_i = x_iP definiert sind, mit P als Gesamtdruck.

Einsetzen in G = Σ n_iµ_i ergibt einen Ausdruck für die Gibbsenergie einer idealen Mischung:

G = Σ n_iµ_i° + RT Σ n_i ln x_i + Σ n_i RT ln ^P/_p°
= n_t [Σ x_iµ_i° + RT Σ x_i ln x_i + RT ln ^P/_p°]

wobei n_t = Σ n_i die Gesamtmenge des Gases im System repräsentiert.

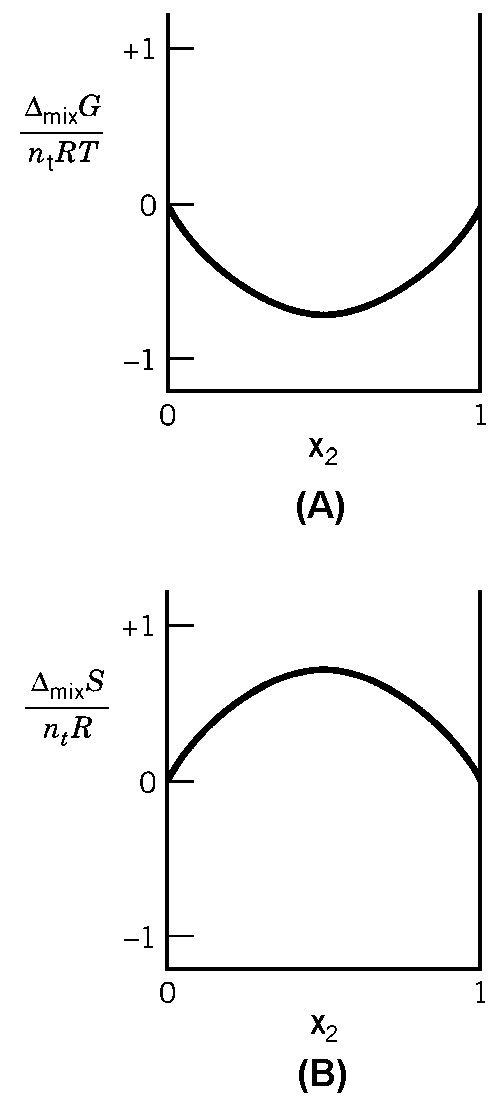Abb. 1: Änderung der Freien Enthalpie (a) und der Entropie (b) als Funktion des Molenbruchs einer zweikomponentigen Mischung.

Vor der Mischung sollen sich die Gase in getrennten Kammern bei gleichem Druck p befinden. Dafür ist G = Σ_i n_i(µ_i° + RT ln ^P/_p°). Für die Änderung der Freien Enthalpie Δ_mixG erhalten wir:

Δ_mixG = G_nachher− G_vorher= n_tRT Σ_i x_i ln x_i

Da die Molenbrüche kleiner als eins sind, ist der Logarithmus negativ und Δ_mixG < 0. Dies gibt die Tatsache wieder, dass das Mischen von Gasen ein spontaner Prozess ist: Wenn zwei Gase zusammengeführt werden, dann diffundieren sie in einander und die Gasphase wird makroskopisch homogen.
In der Abbildung ist die Änderung der Gibbschen Energie für die Mischung zweier Gase als Funktion des Molenbruchs einer Spezies dargestellt. Das Minimum liegt bei x₁ = x₂ = ½ . Die entsprechende Abhängigkeit der Entropie ist der unteren Darstellung zu entnehmen.

Es wird (bei idealen Gasen) keine Wärme erzeugt oder verbraucht, da bei idealen Gasen keine Anziehungs- oder Abstoßungskräfte wirken. Energetisch macht es keinen Unterschied, ob die Gase vermischt oder getrennt sind. Die Triebkraft für die Vermischung rührt von der Entropie her. Hier noch der mathematische Beleg für diese Aussage:

Wegen (^∂G/_∂T)_p,n = -S erhalten wir für eine Mischung idealer Gase Δ_mixS = -(∂Δ_mixG/∂T) = - nRΣ_ix_i ln x_i .

Das Maximum liegt für 2 Komponenten bei x₁ = x₂ = ¹/₂. Die Mischungsenthalpie Δ_mixH können wir über ΔG = ΔH - TΔS berechnen: Δ_mixH = Δ_mixG + TΔ_mixS = 0, d.h. die Energie ändert sich nicht. Treibende "Kraft" für die Durchmischung ist die Entropie und nicht die Energie.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.