Phasengleichgewichte zwischen
Flüssigkeit und Dampf im Zweistoffsystem

Sind in einem System zwei Komponenten vorhanden, K = 2, dann ist nach der Gibbschen Phasenregel, F = K - P + 2, die Anzahl der Freiheitsgrade

Bei konstanter Temperatur bleiben noch (3 - P) - Freiheitsgrade, also maximal 2 für eine Phase, übrig. Dies sind der Druck und die Zusammensetzung, d.h. der Molenbruch. Wir können daher Phasendiagramme konstruieren, bei denen der Druck als Funktion des Molenbruchs dargestellt wird (Dampfdruckdiagramme). Entsprechend kann man bei konstantem Druck ein Phasendiagramm angeben, bei dem die Abhängigkiet der Temperatur von der Zusammensetzung dargestellt ist (Siedediagramm). Solche Diagramme helfen uns, die Vorgänge bei der Destillation zu verstehen.
 

1. Dampfdruckdiagramm

Der Dampfdruck p einer idealen Mischung setzt sich aus den Partialdrücken p_A und p_B der beiden Komponenten A und B zusammen:

Nach dem Raoultschen Gesetz sind die Partialdrücke dieser idealen Mischung über die Drücke p_A* und p_B* der reinen Substanzen, d.h. entweder nur A oder nur B, mit den Molenbrüchen x_A bzw. x_B in der Lösung verknüpft:

Der Dampfdruck als Funktion des Molenbruchs der Substanz A in der Lösung A + B ist dann:

Er ist also linear von x_B abhängig. Falls nun der Dampfdruck von A und B gleich groß sein sollte, dann werden wir in der Gasphase exakt die gleichen Zusammensetzungen wie ín der flüssigen Phase vorfinden. Da jedoch im Allgemeinen eine der beiden Substanzen einen höheren Dampfdruck (wir nennen sie einfach B) als die andere Substanz (also A) haben wird, also r = p_B*/p_A* > 1 gilt, werden wir in der Gasphase eine Anreicherung der flüchtigeren Substanz, also von B, erwarten können. Wenn wir den Molenbruch in der Gasphase durch den Buchstaben y kennzeichnen, dann gilt nach dem Daltonschen Gesetz:

Wir halten also p  =  p_B/y_B  =  p_B* x_B/y_B.

Gleichsetzen dieser Gleichung  mit  p  =  p_A* + (p_B* - p_A*) x_B und Auflösen nach y_B liefert:

Für r > 1 folgt aus dieser Gleichung unmittelbar unsere Aussage, dass y_B > x_B ist. Wir können nun den Gesamtdruck p auch durch den Molenbruch in der Gasphase, y_B, ausdrücken, indem wir unsere letzte Gleichung nach x_B auflösen und in die Gleichung für p(x_B) einsetzen:
 

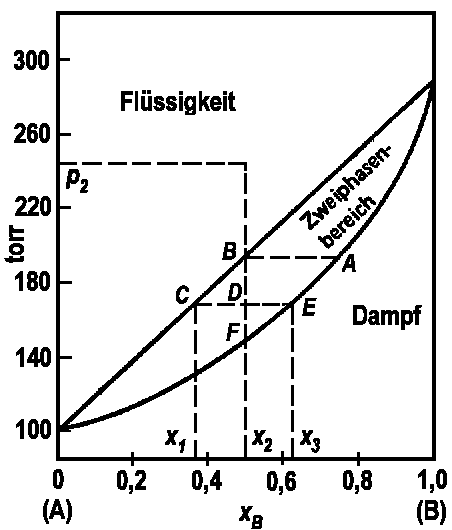Abb. 1: Abhängigkeit des Dampfdrucks von der Zusammensetzung (Molenbruch) bei 60°C für das System 2-Methylpropanol-1 (A) / Propanol-2 (B). Diese beiden Alkohole bilden praktisch ideale Mischungen.

In der Abbildung 1 ist der Dampfdruck über einem System aus 2-Methylpropanol-1 und Propanol-2 dargestellt. Dieses System gehorcht dem Raoultschen Gesetz ziemlich streng über den gesamten Zusammensetzungsbereich. Die ansteigende Gerade in diesem Diagramm stellt die Abhängigkeit des Gesamtdrucks p(x_B) über der Lösung vom Molenbruch in der Flüssigkeit dar. Die gekrümmte untere Kurve stellt die Abhängigkeit des Druckes von der Zusammensetzung des Dampfes dar, p(y_B).

Wir wollen nun eine Flüssigkeit der Zusammensetzung x₂ beim Druck p₂ betrachten. Dieser Punkt liegt an einer Stelle, wo das System nur aus einer Phase besteht, also 3 Freiheitsgrade besitzt. Einer dieser Freiheitsgrade ist schon durch die Forderung vergeben, dass das Diagramm für konstante Temperatur gilt. Bei jeder willkürlich gewählten Zusammensetzung x₂ kann also die flüssige Lösung bei konstanter Temperatur über einen bestimmten Druckbereich existent sein. Reduziert man den Druck entlang der gestrichelten Linie bei konstanter Zusammensetzung, dann passiert so lange nichts, bis bei B die Dampfdruckkurve erreicht wird. An diesem Punkt beginnt die Flüssigkeit zu verdampfen. Der gebildete Dampf hat sich gegenüber der Flüssigkeit an der flüchtigeren Komponente, dem Propanol-2, angereichert. Die Zusammensetzung der zuerst gebildeten kleinen Dampfmenge wird durch den Punkt A auf der Dampfdruckkurve wiedergegeben.

Wenn man den Dampfdruck noch etwas weiter unter den Punkt B verringert, dann befindet man sich in einem Zweiphasenbereich des Diagramms. In diesem Bereich sind Flüssigkeit und Dampf koexistent. Die gestrichelte Linie, die horizontal durch einen typischen Punkt B im Zweiphasendiagramm läuft, nennt man eine Verbindungslinie. Diese Isobare verbindet die beiden Punkte, die die Zusammensetzung der im Gleichgewicht stehenden flüssigen und Dampfphase angeben.

Im Zweiphasenbereich (P = 2) ist F = 2. Einen der beiden Freiheitsgrade haben wir schon für die Forderung konstanter Temperatur geopfert, es bleibt also nur noch einer übrig. Legen wir in diesem Bereich den Druck fest, dann ist damit zugleich auch die Zusammensetzung sowohl der flüssigen als auch der Dampfphase eindeutig festgelegt; ihre Zahlenwerte ergeben sich als die Schnittpunkte der Verbindungslinie (Isobaren) mit der Dampfdruckkurve und der Kondensationsdruckkurve.

Die Zusammensetzung des gesamten Systems im Punkt D im Zweiphasenbereich ist x₂; sie ergibt sich aus der Zusamamensetzung x₁ der flüssigen und der Zusammensetzung x₃ = y_B der Dampfphase. Wir können die relativen Mengen von Flüssigkeit und Dampf berechnen, die diese Bruttozusammensetzung ergeben. Wenn wir mit n_l die Summe der Molenphase der beiden Komponenten A und B in der flüssigen und mit n_g die Molzahl in der Dampfphase bezeichnen, dann erhalten wir unter Berücksichtigeung der Stoffkonstanz für die Komponente B:

Diesen Ausdruck nennt man Hebelregel. Sie gilt für jedes durch eine Verbindungslinie verknüpfte Zusammensetzungspaar, das wiederum zu zwei sich im Gleichgewicht stehenden Phasen in einem Zweikomponentensystem gehört. Wenn das Diagramm in Massen- statt Molenbrüchem aufgetragen ist, dann ergibt das Verhältnis der Abschnitte auf der Verbindungslinie das Massenverhältnis der beiden Phasen an.

Wenn man den Druck entlang der Linie BF noch weiter veringert, dann verdampft immer mehr von der flüssigen Phase, bis schließlich bei F keine Flüssigkeit mehr vorhanden ist: Das System besteht nur noch aus der Dampfphase (p = 1).

2. Siedediagramme
 

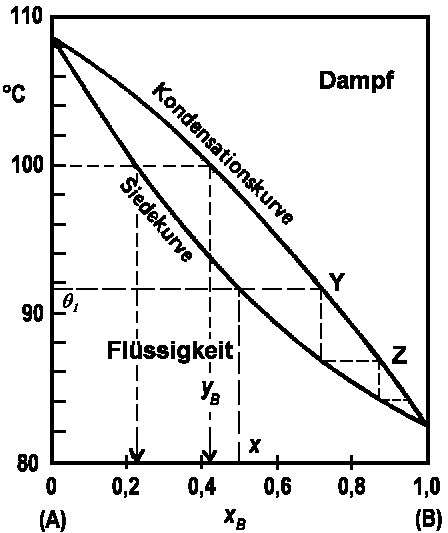Abb. 2: Abhängigkeit der Siede- und Kondensations- temperatur von der Zusammensetzung beim System 2-Methylpropanol-1 (A)/ Propanol-2 (B). Diese beiden Alkohole bilden nahezu ideale Lösungen.

Das isobare Temperatur-Zusammensetzungs-Diagramm eines im Gleichgewicht befindlichen Zweiphasensystems ist nichts anderes als die Siedepunktskurve von Mischungen unterschiedlicher Zusammensetzung bei einem willkürlich gewählten, konstantem Druck. Wenn der äußere Druck 10⁵ Pa beträgt, dann zeigt das Diagramm die normalen Siedepunkte. Abbildung 2 zeigt ein solches Diagramm für ein System aus 2-Methylpropanol-1 und Propanol-2.

Die Siedekurve einer idealen Mischung kann berechnet werden, wenn die Dampfdrücke der reinen Komponenten als Funktion der Temperatur bekannt sind. Die beiden Endpunkte der Siedekurve in der Abbildung 2 bedeuten die Temperaturen, bei denen die reinen Komponenten einen Dampfdruck von 760 torr besitzen, nämlich 82,3°C und 108,5°C. Die Zusammensetzung einer Mischung, die irgendwo zwischen diesen beiden Temperaturen, z.B. bei 100°C, siedet, findet man folgendermaßen:

Wenn x_A der Molenbruch des 2-Methylpropanol-1 ist, dann gilt nach dem Raoultschen Gesetz:

Bei 100°C beträgt der Dampfdruck des Propanols 1440 torr, der 2-Methylpropanols-1 570 torr. Es ist also 760 = 570 x_A + 1440 (1 - x_A) oder x_A = 0,781 und x_B = 0,219. Damit haben wir schon einen Punkt auf der Siedekurve bestimmt; die anderen lassen sich in derselben Weise berechnen.

Die Zusammensetzung des Dampfes läßt sich aus dem Raoultschen Gesetz bestimmen:

Die Zusammensetzungskurve für den Dampf (Kondensationskurve) kann man also leicht aus der Siedekurve konstruieren.
 

3. Fraktionierte Reaktion

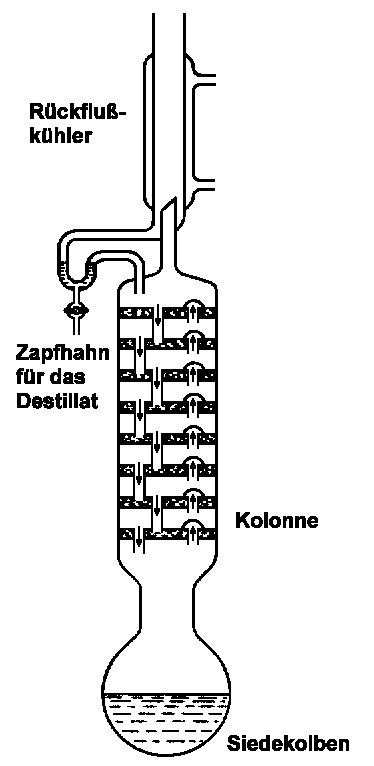Abb. 3: Überlaufkolonne für die fraktionierte Destillation

Die Anwendung des Siedediagramms für eine vereinfachte Darstellung des Destillationsvorgang zeigt Abbildung 3 in Verbindung mit Abb. 2. Eine Lösung der Zusammensetzung X beginnt bei der Temperatur θ₁ zu sieden (Abb.2). Die erste sich bildende Dampfmenge hat die Zusammensetzung Y und ist mit der flüchtigeren Komponente etwas angereichert. Wenn diese kleine Dampfmenge kondensiert und erneut bis zum Sieden erhitzt wird, dann hat der daraus wieder entstehende Dampf die Zusammensetzung Z. Dieser Vorgang wird so lange wiederholt, bis das Destillat aus der (nahezu) reinen Komponente B besteht. (Theoretisch gelangt man niemals zu den völlig reinen Komponenten.) In der Praxis überdecken die aufeinanderfolgenden Fraktionen natürlich einen bestimmten Zusammensetzungsbereich, die vertikalen Linien in Abb. 2 können jedoch als repräsentant für die Durchschnittszusammensetzung innerhalb dieser Bereiche angesehen werden.

Eine Fraktionierkolonne (Abb.3) ist eine Vorrichtung, die die aufeinanderfolgenden Kondensations- und Verdampfungsschritte, durch die eine fraktionierte Destillation charakterisiert ist, automatisch durchführt. Ein besonders einleuchtendes Beispiel ist der in der Abbildung 3 gezeigte Typ einer Kolonne mit "Blubberhütchen". Der vom Siedekolben aufsteigende Dampf blubbert durch eine dünne Flüssigkeitsschicht auf der ersten Platte. Diese Flüssigkeit ist etwas kühler als die im Siedekolben, so dass eine partielle Kondensation stattfindet. Der Dampf, der von der ersten Platte aufsteigt, ist daher gegenüber dem ursprünglichen Dampf mit der flüchtigeren Komponente angereichert. Eine ähnliche Anreicherung findet an jeder aufeinanderfolgenden Platte statt. Jeder Gleichgewichtseinstellung zwischen Flüssigkeiten und Dampf entspricht eine der Stufen in Abbildung 2.

Die Wirksamkeit einer solchen Destillationskolonne wird durch die Zahl solcher Gleichgewichtsstufen gemessen, die durch die Kolonne erreicht werden können. Jede solcher Stufen nennt man einen theoretischen Boden. In einer gut entworfenen Blubberkolonne wirkt jede dieser Einheiten nahezu wie ein theoretischer Boden. Wir können also die Wirksamkeit verschiedener Arten gepackter Kolonnen stets durch die Zahl ihrer theoretischer Böden angeben. Die destillilative Trennung von Flüssigkeiten, deren Kochdruckpunkte nahe beieinanderliegen, ist nur mit einer Kolonne möglich, die eine beträchtliche Zahl theoretischer Böden besitzt.



4. Azeotrope
 

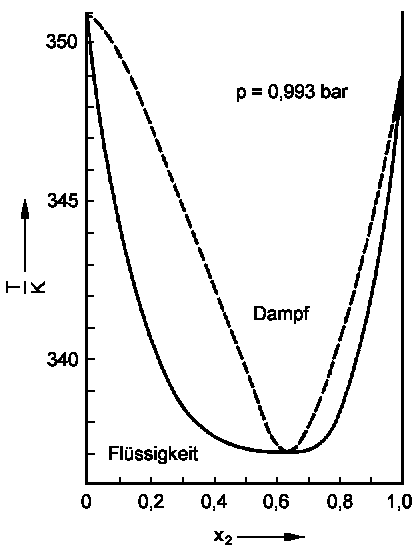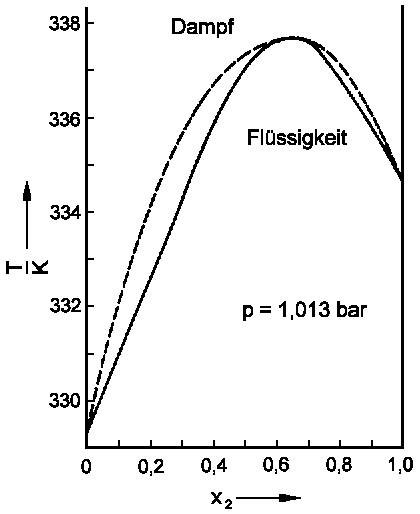
Abb. 4: T, x-Diagramm des Systems Propanon / Trichlormethan (Index 2) bei p = 1,013 bar.	Abb. 5: T, x-Diagramm des Systems Ethanol / Tetrachlormethan (Index 2) bei p = 0,993 bar.

Wenn wir es nicht mit einem idealen System zu tun haben, können wir die Siedediagramme nicht mehr so einfach berechnen. Wir wollen uns deshalb darauf beschränken, eine qualitative Diskussion für die Fälle durchzuführen, die bei den p, x-Diagrammen zum Auftreten von Extremwerten geführt haben. In den Abbildungen 4 und 5 sind die der Abbildung 2 entsprechenden Siedediagramme wiedergegeben.

Wir erkennen, dass dem Dampfdruckminimum eine Siedepunktmaximum und dem Dampfdruckmaximum ein Siedepunktminimum entspricht. Die Extremwerte bezeichnet man wieder als azeotrope Punkte. Ihr Auftreten hat starke Auswirkungen auf die Möglichkeiten einer destillativen Trennung. Da sich das azeotrope Gemisch wie ein reiner Stoff verhält, kann man keine Trennung in die beiden Stoffe erzielen

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.