Barometrische Höhenformel

Wie groß ist die Anzahldichte Ñ = N/V von Molekülen in einem Gravitationsfeld, wenn man von einer konstanten Temperatur T (isotherme Atmosphäre) ausgeht?
Die potentielle Energie eines Teilchens im Gravitationsfeld ist E = m · g · h  und nach der Boltzmannschen Energieverteilung erhalten wir sofort
 
 

Ñ(h)  ~ e-mgh/kT

oder
Ñ(h)  = Ñ(h=0) e-mgh/kT
p(h)  =  po e-mgh/kT
mit po = p(h=0).

Wir können diese Formel natürlich auch ohne Kenntnis der Boltzmannschen Energieverteilung herleiten:
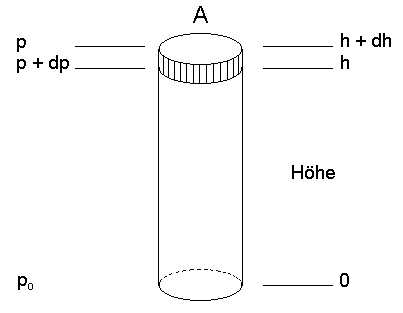Abb. 1: Der Druck p nimmt um dp zu, wenn in einer Luftsäule die Höhe h um dh erniedrigt wird.
Dazu stellen wir uns eine Luftsäule der Höhe h vor (s. Abb.) und fragen danach, wie sich der Druck p ändert, wenn wir die Höhe infinitesimal um dh ändern. Es gilt

p  =  F/A =  m · g/A  =  ρV· g/A  =  ρ·h·g

(F = Kraft;  ρ = Dichte, A = Fläche)

→ dp  =   −ρ·g·dh.

Der Druck nimmt ab, wenn die Höhe zunimmt.

Mit M = Molekulargewicht gilt

ρ  =  m/V  =  Mn/V =  p· M/RT

Einsetzen von ρ  in die Gleichung für dp ergibt:

 dp  =  −p ·(M/RT)· g ·dh

Division durch p gewährleistet, dass die linke Seite nur von p, die rechte nur von h abhängt:

po∫p dp/p  =  −(Mg/RT)o∫hdh         →          ln (p/po)  =  − (Mg/RT)· h,

was genau unserer eingangs abgeleiteten Barometrischen Höhenformel entspricht, wenn wir von Mol auf ein Teilchen umrechnen (R → k und M → m).

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.