Stöße

Mit Hilfe der kinetischen Gastheorie können wir berechnen, wie häufig Teilchen zusammenstoßen und welchen Weg sie im Mittel zwischen zwei Stößen zurücklegen.
 

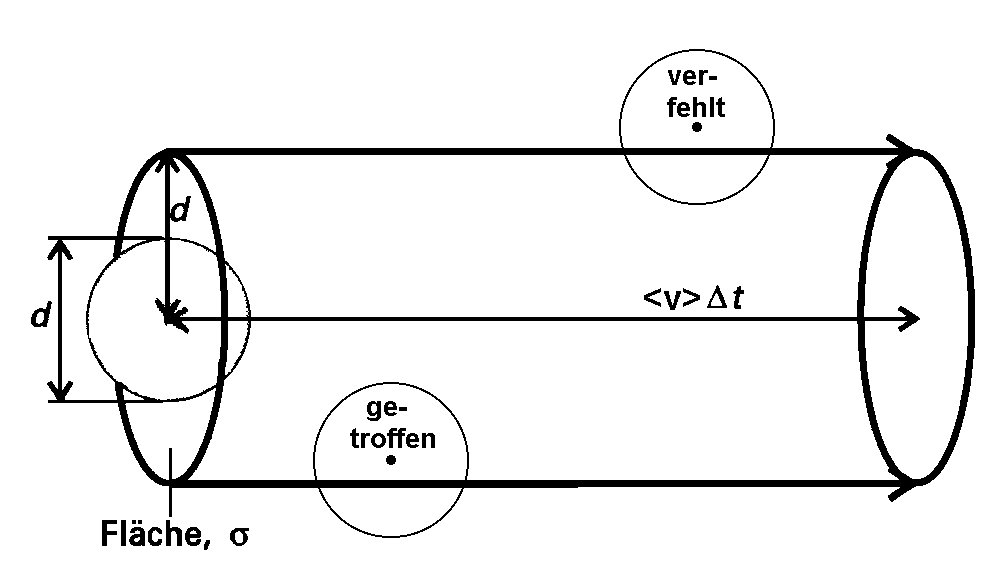Abb. 1: Der Stoßzylinder für ein Molekül mit dem Durchmesser d während einer Zeit Δt hat die Gestalt eines Kreiszylinders mit dem Radius d und der Länge <v>Δt. Jede Begegnung mit einem Molekül, dessen Mittelpunkt innerhalb des Stoßzylinders liegt, führt zu einem Treffer. In Wirklichkeit ist der Zylinder nicht gerade, sondern ändert bei jedem Stoß seine Richtung. Sein Volumen wird davon jedoch nicht beeinflußt, so dass wir ihn in unseren Rechnungen vereinfacht als gerade auffassen können.

Wir wollen immer dann von einem Stoß sprechen, wenn die Zentren zweier Teilchen sich einander bis auf einen Abstand d nähern, wobei d von der Größenordnung des Teilchendurchmessers ist (bei harten Billardkugeln ist d deren Durchmesser). Für die Berechnung stellen wir uns vor, dass alle Teilchen bis auf eines an ihren Positionen eingefroren sind, und wir beobachten jetzt, was passiert, wenn das bewegliche Teilchen während der Zeit Δt mit der Geschwindigkeit <v> durch das Gas fliegt. Auf seinem Flug überstreicht es einen Zylinder mit dem Stoßquerschnitt σ = πd² und der Länge <v>Δt, also mit dem Volumen σ<v>Δt (siehe Abb. 1). Befindet sich das Zentrum eines anderen Teilchens innerhalb dieses Zylinders, so erfolgt ein Stoß. Die Anzahl der ruhenden Teilchen, deren Zentren innerhalb des Stoßzylinders liegen, ist gleich dem Produkt aus dem Volumen des Zylinders und der Teilchendichte Ñ, also gleich σ<v>Δt Ñ. In der Zeit Δt erfolgen gerade so viele Stöße, wie diese Zahl angibt. Die Stoßzahl z (engl. collision frequency), also die Anzahl der Stöße pro Zeit, ist demnach gleich σ<v>Ñ. In Wirklichkeit sind die anderen Teilchen nicht in Ruhe, wir müssen daher die Relativgeschwindigkeit der stoßenden Teilchen und nicht ihre absolute Geschwindigkeit einsetzen. Die Relativgeschwindigkeit zwischen zwei Teichen A und B erhalten wir, wenn die Masse m durch die reduzierte Masse µ ersetzt wird:
 

Wir können nun die mittlere freie Weglänge λberechnen. Wenn ein Teilchen z Stöße pro Zeiteinheit erleidet, dann verbringt es die Zeit 1/z im freien Fluge zwischen zwei Stößen zurück und legt dabei die Strecke (1/z)<v> zurück. Die mittlere freie Weglänge ist daher gegeben durch
 

λist also dem Druck umgekehrt proportional.

Die Stoßzahl z gibt an, wie viele Stöße ein Teilchen pro Zeiteinheit erleidet. Multipliziert man z mit ½Ñ, so erhält man die Anzahl aller Stöße pro Zeiteinheit und pro Volumeneinheit zwischen den Teilchen eines Gases. Der Faktor ½ gewährleistet, dass die Stöße A₁...A₂ und A₂...A₁ nur einmal gezählt werden. Die Anzahl der Stöße pro Zeiteinheit und pro Volumeneinheit ist

Nach Eingeben der mittleren Geschwindigkeit erhalten wir:
 

Die Tabelle gibt einige typische Werte für die Stoßquerschnitte wieder.
 

Wenn es sich um Stöße zwischen unterschiedlichen Molekülen 1 und 2 handelt, ist der Stoßquerschnitt ebenfalls durch σ = πd² gegeben, aber mit d = ½ (d_A + d_B). Ein Teilchen der Sorte A erleidet in der Zeiteinheit mit N_B Teilchen der Sorte B  z_AB = σ<v_rel>N_B/V Stöße. Weil es insgesamt N_A Teilchen der Sorte A gibt, ist die Gesamtzahl der Stöße A-B in der Zeiteinheit (σ<v_rel>N_B/V)N_A; die Gesamtzahl der Stöße A-B in der Zeit- und Volumeneinheit beträgt:
 

mit [A] = n_A/V und [B] = n_B/V

Stöße von Teilchen an Oberflächen

Es werden alle Teilchen in dem Volumen Av_xΔt, die eine positive Geschwindigkeitskomponente v_x haben, innerhalb der Zeitspanne Δt an die Wand stoßen. Die mittlere Zahl aller Stöße in diesem Zeitabschnitt ist dann gleich dem Mittelwert dieser Größe multipliziert mit der Teilchendichte (^N/_V):

Die Anzahl der Stöße mit der Oberfläche pro Zeiteinheit und pro Flächeneinheit ist dann
 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.