Reaktion n-ter Ordnung

Die DGL für eine beliebige Reaktionsordnung n können wir nun aufstellen (n kann auch eine gebrochene Zahl sein; nur n = 1 ist eine Ausnahme):

− d[A]/dt  =  kn[A]n

und nach bewährtem Schema lösen:
d[A]/[A]n  = −kndt

Integration unter der Annahme, dass zur Zeit t = 0  [A] = [A]0 ist, führt zu
 

 oder

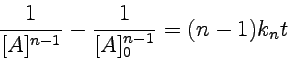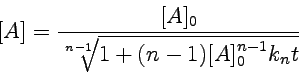Für die Halbwertszeit t½ ist [A]/[A]o = 1/2. Einsetzen ergibt:

2n-1  =  1 + (n - 1) [A]on-1 kn t½
t½  =  {2n-1− 1}/{(n − 1) [A]on-1 kn}

was eine üble Abhängigkeit von der Ausgangskonzentration verdeutlicht. Für n = 2 finden wir sofort

t½  (2. Ordnung)  =  1/[A]o k2

Ein kleiner Ausflug für den mathematisch Interessierten zeigt, dass auch für n = 1 die Gleichung für [A] richtig ist (wenn auch jeder Hochleistungsrechner aussteigt):
Zunächst setzen wir n = 1 + z und fragen welche Gestalt die Gleichung für den Limes z → 0 annimmt:

[A]o/[A]  =  (1 + z [A]oz k1t)1/z

Für z → 0 wird [A]0z = 1, da jeder Wert (größer Null) hoch Null eins ergibt. Es bleibt also

[A]o/[A]  =  limz→o(1 + z k1t)1/z

Dies ist aber die Definition der Exponentialfunktion, so wie sie vielleicht manche von der Schule oder von der Zinseszins-Rechnung kennen. Wir erhalten also

[A]o/[A]  =  e k1 t

oder
[A]  =  [A]o e−k1 t
 
 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.