Das kinetische Experiment liefert zunächst nur verschiedene Konzentrationswerte einer Substanz A zu verschiedenen Zeiten. Der theoretische Ausdruck für die zeitliche Änderung der Substanz als Funktion der Konzentrationen aller N Reaktionsteilnehmer hat jedoch die allgemeine Form:
dcA/dt = f (cA, cB, ..., cN)
Die Reaktionsgeschwindigkeit, also die zeitliche Abnahme de Konzentration eines Ausgangsstoffes A, hängt oft vom Produkt einer Anzahl von Konzentrationen ab. Für einen solchen Fall gilt:
−dcA/dt = k cAa · cBb... cNn
Die Reaktionsordnung ist definiert als die Summe der Exponenten der Konzentrationsausdrücke in diesem Gesetz.
Für den Fall des Distickstoffpentoxids, 2N2O5→
4NO2 + O2, wurde die folgende Gesetzmäßigkeit
im Experiment beobachtet:
| − d[N2O5]/dt = k1 [N2O5] |
In dieser Beziehung bedeuten die eckigen Klammern, wie üblich,
molare Konzentrationen. Nach unserer Definition handelt es sich hier also
um eine Reaktion 1. Ordnung, da der Exponent 1 ist. Der Zerfall
des Stickstoffdioxids, 2NO2 →
2NO + O2, gehorcht dem Gesetz:
| − d[NO2]/dt = k2 [NO2]2 |
Dies ist eine Reaktion 2. Ordnung. Dieses Beispiel zeigt auch, dass Zerfallsreaktionen mit nur einem Ausgangsstoff durchaus nicht immer einem Geschwindigkeitsgesetz 1. Ordnung gehorchen müssen. Wir müssen uns immer verdeutlichen, dass das empirische Geschwindigkeitsgesetz in der Regel die molekularen Details nicht widerspiegeln kann.
Die Reaktionsgeschwindigkeit von
Diese Reaktion ist 1. Ordnung in Bezug auf CO, 1. Ordnung in Bezug auf N2O und daher insgesamt 2. Ordnung.
Der Zerfall des Acetaldehyds in der Gasphase bei 450°C, CH3CHO → CH4 + CO, gehorcht der folgenden Gleichung:
− d[CH3CHO]/dt = k1,5 [CH3CHO]3/2
Diese Reaktion ist also von der Ordnung 1,5 . Die Reaktionsordnung braucht demnach keine ganze Zahl zu sein; es gibt auch Reaktionen mit gebrochener Ordnung.
Die Geschwindigkeit der Emulsionspolymerisation des Styrols wird nach der Anlaufperiode unabhängig von der Monomerkonzentration. Es gilt also:
- d[M]/dt = k0 [M]0 = k0
Gemäß unserer Definition ist diese Reaktion also 0. Ordnung. Dasselbe gilt für die Photosynthese in grünen Pflanzen in Gegenwart von Chlorophyll als Katalysator. Die Bildungsgeschwindigkeit der Glucose ist unabhängig von der Konzentration an CO2 und Wasser. Der Assimilierungsvorgang ist sowohl in Bezug auf die einzelnen Ausgangsstoffe als auch insgesamt 0. Ordnung. Ähnliches gilt für andere katalysierte Reaktionen.
Wir haben gesehen, dass die empirisch aus experimentellen Daten bestimmte Reaktionsordnung nicht notwendigerweise ganzzahlig sein muss. Besonders wichtig ist die Tatsache, dass zwischen der Form der stöchiometrischen Gleichung und der Reaktionsordnung kein notwendiger Zusammenhang besteht. So haben die Zerfallsgleichungen für N2O5 und NO2 dieselbe Form; dennoch ist die eine Reaktion 1. Ordnung und die andere 2. Ordnung.
Die Dimension der Geschwindigkeitskonstanten hängt von der Reaktionsordnung ab. Für Reaktionen 1 Ordnung ist −dc/dt = k1c; die Konstante hat also die Dimension einer reziproken Zeit, z.B. s-1. Für Reaktionen 2. Ordnung gilt −dc/dt = k2c2; solche Konstanten haben also die Dimension [Konzentration]-1·[Zeit]-1, z.B. l·mol-1·s-1 oder cm3·Moleküle-1·s-1. Allgemein ausgedrückt hat die Konstante kn für eine Reaktion n-ter Ordnung die Dimension [Konzentration]1-n ·[Zeit]-1.
Weder die stöchiometrische Gleichung noch das Geschwindigkeitsgesetz einer Reaktion können uns zuverlässige Aussagen über den tatsächlichen Mechanismus dieser Globalreaktion machen. Die gesamte chemische Reaktion setzt sich aus mehreren Zwischenstufen zusammen. Jeden Einzelschritt in einer komplexen zusammengesetzten Reaktion nennt man Elementarreaktion. Wenn eine solche Elementarreaktion der spontane Zerfall eines Moleküls ist, dann nennt man sie unimolekular. Ist für das Zustandekommen der Elementarreaktion ein Zusammenstoß zweier Moleküle notwendig, dann nennen wir die Reaktion bimolekular. Wir sehen also, dass der Begriff der Reaktionsmolekularität sinnvoll nur auf die Teilvorgänge (Elementarreaktionen) einer komplexen Reaktion angewandt werden kann.
Nur dann, wenn man die Elementarreaktion kennt, kann man aus der Reaktionsgleichung auch das Geschwindigkeitsgesetz ableiten. So ist z.B. die Reaktion CO + N2O → CO2 + N2 eine echte bimolekulare Reaktion.
Diese Reaktion zwischen CO und N2O der folgenden Beziehung muss daher
−d[CO]/dt = k2 [CO] [N2O]
Dies ist eine Reaktion 2. Ordnung. Alle bimolekularen Elementarreaktionen sind 2. Ordnung. Die Umkehrung dieses Satzes ist falsch; es gibt zahlreiche Reaktionen 2. Ordnung, die nicht bimolekular verlaufen (weil sie sich in Wirklichkeit aus vielen Elementareaktionen zusammensetzen).
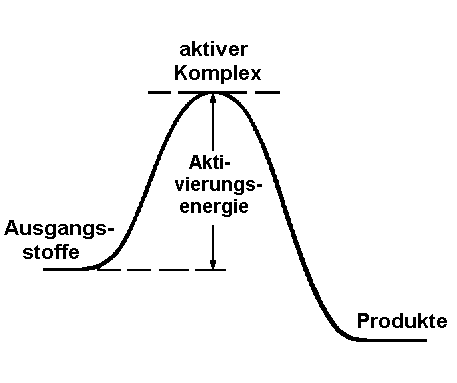 |
| Abb. 1: Die Moleküle müssen bei einer chemischen Reaktion eine Energiebarriere überwinden |
Bei bimolekularen Reaktionen treten zwei Moleküle mit hinreichender kinetischer Energie zu einem aktivierten Komplex zusammen. Diesen Vorgang zeigt schematisch nebenstehende Abbildung. Ausgangsstoffe und Reaktionsprodukte befinden sich in einem Minimum der potentiellen Energie, also in einem stabilen Zustand; bei jeder Elementarreaktion müssen die reagierenden Moleküle über den Wall der Aktivierungsenergie hinwegkommen, dessen Maximum durch die Energie des labilen aktivierten Komplexes gekennzeichnet ist.
Bei unimolekularen Reaktionen besteht der "aktivierte Komplex" aus einem hochangeregten Molekül, das spontan zerfällt. Ein gutes Beispiel für eine physikalische, unimolekulare Reaktion ist der radioaktiver Zerfall, z.B. Ra → Rn + α. An jedem Zerfall ist nur ein einziger Atomkern beteiligt; für die Zerfallsgeschwindigkeit gilt die folgende Beziehung:
−dN/dt = k1 N
Hierin bedeutet N die Zahl der zu einem beliebigen Zeitpunkt vorhandenen
Radiumatome. Die Zerfallsgeschwindigkeit ist also stets proportional der
im Beobachtungszeitpunkt noch nicht zerfallenen Atome.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.