Folgereaktionen

Folgereaktionen A → B → C

In den einfachsten Fällen ist es möglich, die Bildungs- oder Zerfallsgeschwindigkeit der Ausgangs-, Zwischen- und Endprodukte einer Reaktionsfolge mathematisch geschlossen abzuleiten. Die Bildung eines Stoffes C aus A über ein Zwischenprodukt B als Folge zweier irreversibler Prozesse 1. Ordnung

	k		k'
A	→	B	→	C

soll als einfaches Beispiel eingehender diskutiert werden: Die Ausgangskonzentrationen bei t = 0 seinen [A]_obzw. [B]_o = 0 und [C]_o = 0. Für die Zerfalls- bzw. Bildungsgeschwindigkeiten müssen wir dann ansetzten:

^d[A]/_dt = − k [A]

^d[B]/_dt = k[A] − k'[B]

^d[C]/_dt = k'[B]

Die Lösung für [A] kennen wir bereits:

[A] = [A]_o e^−kt

Die Konzentration [A] des Ausgangstoffes A nimmt wie bei jeder Reaktion erster Ordnung exponentiell mit der Zeit ab. Für [B] ergibt sich damit

^d[B]/_dt = k[A]_o e^−kt − k'[B]

Das ist eine lineare Differentialgleichung erster Ordnung, die sich mit Hilfe der Lagrangeschen Methode der Variation der Konstanten lösen lässt:

Wir integrieren zunächst die homogene Differentialgleichung

^d[B]/_dt + k' [B] = 0

und erhalten dabei [B] = c · e^−k'
t

Dann setzen wir als Lösung für die inhomogene Differentialgleichung an

[B] = c(t) e^−k'
t

und erhalten für die von t abhängige Größe c(t)

c(t) = − ^k[A]o/_k−k'· e^−(k−k')t + konst

so dass die allgemeine Lösung nach Berücksichtigung der Anfangsbedingungen lautet

[B] = ^k[A]o/_k'_−k(e^−k
t − e^−k'
t)

Die Konzentration [C] des Endprodukts C erhalten wir aus der Bilanz

[A]_o = [A] + [B] + [C]

[C] = [A]_o (1 −^k'/_k'−k e^{−k t} + ^k/_k'−k e^−k1't)



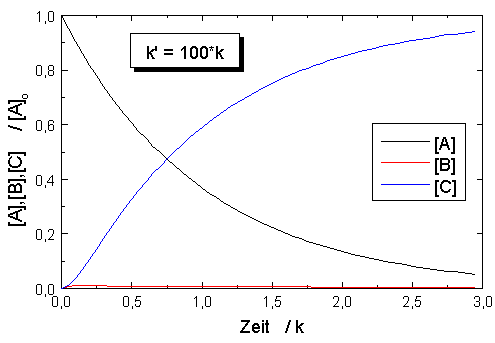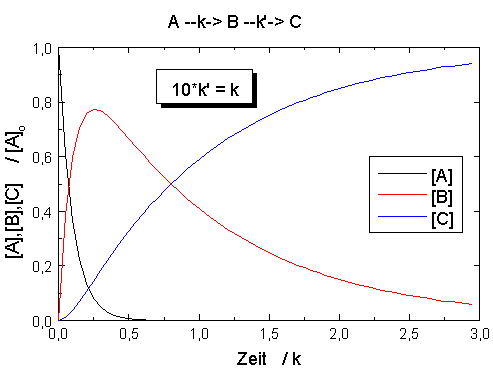
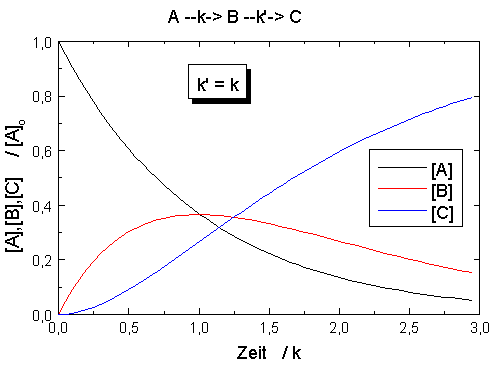
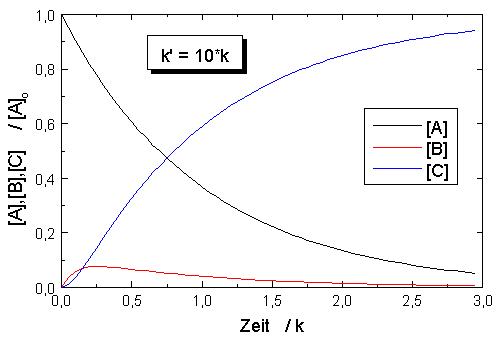
Abb.1: Zeitlicher Verlauf für den Prozess A → B → C mit den Geschwindigkeitskonstanten k bzw. k'. Anfangsbedingungen sind [A]_oaber [B]_o = [C]_o = 0.

In der Abbildung sind die Konzentrationen des Ausgangsstoffes [A], des Zwischenprodukts [B] und des Endprodukts [C] für eine Ausgangskonzentration [A]_o = 1 mol·dm^-3 und verschiedene Verhältnisse der Geschwindigkeitskonstanten k und k'. Der Vergleich der Abbildungen zeigt, dass bei einem großen Wert des Verhältnisses k/k' das Ausgangsprodukt A schnell abgebaut wird und das Zwischenprodukt B intermediär in hoher Konzentration auftritt, während bei einem kleinen Wert dieses Verhältnis A nur langsam verbraucht wird und B nur in geringerer Konzentration vorliegt. Der zeitliche Verlauf der Konzentration des Endproduktes C ändert sich nicht, wenn die Werte von k und k' vertauscht werden, wie auch aus der Gleichung für C hervorgeht. Ein Vergleich der Abbildungen lässt auch erkennen, wie sich bei festgehaltenen Werten von [A]_o und k eine Veränderung von k' auf den zeitlichen Konzentrationsverlauf von B und C auswirkt: Durch eine Verringerung von k' verschiebt sich das Auftreten der Maximalkonzentration von B nach größerer Reaktionszeit und die Induktionszeit bis zum Auftreten merklicher Mengen an Reaktionsprodukt C wird deutlicher.

Als Beispiel für eine Folge von zwei Reaktionen erster Ordnung kann der thermische Zerfall von Aceton dienen, der nach Winkler und Hinshelwood über die Stufen

		O
		\| \|
CH₃	−	C	−	CH₃	→	CH₂	=	CO	+	CH₄
CH₂	=	CO	→	½	C₂H₄	+	CO

verläuft.
Wird das Verhältnis^k/_k' extrem groß oder klein (s. die beiden linken Abb.), d.h. ist k >> k' oder k << k', so geht die Gleichung für C über in

[C] = [A]_o · (1 − e^{−k' t}) wenn k >> k'

oder

[C] = [A]_o · (1 − e^{−k t}) wenn k << k'

Der Reaktionsablauf wird dann allein durch die langsamere der beiden Folgereaktionen bestimmt, die Zeitabhängigkeit der Konzentration [C] entspricht einer Reaktion erster Ordnung.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.