Beim Transport von Ionen in einer Lösung unter Einfluss eines
elektrischen Feldes bewegen sich die Kationen in Richtung der negativ geladenen
Elektrode und die Anionen in Richtung der positiv geladenen Elektrode. Wir wollen uns diesen Mechanismus der Ionenwanderung in Lösung nun
etwas näher ansehen. Auf Ionen in Lösung wirken eine Reihe von
Kräften. Die Ionen erfahren ungeordnete Stöße durch die
benachbarten Moleküle des Lösungsmittels. In einem elektrischen
Feld E erfährt ein Ion mit der Ladung ze eine Kraft mit dem Betrag
F = z e E.
Diese Kraft beschleunigt ein Kation in Richtung der Kathode und ein
Anion in Richtung der Anode. Wenn ein Ion durch das Lösungsmittel
gezogen wird, erfährt es eine Reibungskraft F', die mit zunehmender
Geschwindigkeit immer größer wird und das Ion abzubremsen versucht.
Wenn wir annehmen, dass die Stokessche Gleichung F' = 6πηa
w für eine Kugel mit dem Radius a und der Geschwindigkeit w
auch für so kleine Teilchen wie Ionen gilt, dann wird eine stationäre
Wandergeschwindigkeit erreicht, bei der sich die beschleunigende Kraft
des elektrischen Feldes, F = z e E, und die Reibungskraft F' im Gleichgewicht
befinden (F=F'):
w = zeE/6πηa
Die Wanderungsgeschwindigkeit w bestimmt, wie schnell die Ladungen transportiert
werden; wir können also erwarten, dass die Leitfähigkeit
abnimmt, (a) wenn die Viskosität größer wird, und (b) wenn
die Ionen größer werden.
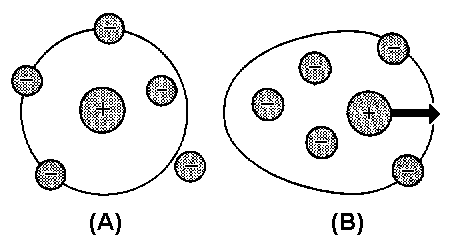 |
| Abb. 1: (a) Wenn kein äußeres Feld angelegt wird, ist die Ionen-Atmosphäre um ein zentrales positives Ion kugelsymmetrisch. (b) Ein elektrisches Feld deformiert die Ionen-Atmosphäre; die Zentren der positiven und negativen Ladungen fallen nicht mehr zusammen. Dadurch wird die Bewegung des Zentralions gebremst. |
Experimentell lassen sich diese Voraussetzungen für große Ionen wie R4N+ oder RCOO- bestätigen, nicht aber für kleine Ionen. Man kann diese Diskrepanz deuten, wenn man den hydrodnamischen (effektiven) Radius eines Ions einführt, bei dem berücksichtigt wird, dass ein Ion bei seiner Wanderung eine Reihe von Lösungsmittelmolekülen mit sich führt (Abb. 1a). Kleine Ionen haben stärkere elektrische Felder um sich herum als große, denn das elektrische Feld auf der Oberfläche einer Kugel mit dem Radius R ist proportional z e/R². Kleine Ionen sind stärker solvatisiert als große. Ein Ion mit kleinem Ionenradius, das bei seiner Wanderung viele Lösungsmittelmoleküle mit sich schleppt, hat einen großen hydrodynamischen Radius, und seine molare Leitfähigkeit ist kleiner als die eines größeren Ions mit derselben Ladung. Tatsächlich sind die Verhältnisse noch etwas komplizierter, wenn man die Abbildung 1 ansieht.
Die Wanderungsgeschwindigkeit w ist in jedem Fall der Stärke des
angelegten Feldes E proportional. Den Proportionalitätsfaktor nennt
man Beweglichkeit u eines Ions:
| w = u E |
In der nachfolgenden Tabelle sind einige Zahlenwerte von Ionen-Beweglichkeiten
angegeben. Sie liegen meist um 6 · 10-4 cm2.s-1.V-1.
Das bedeutet, wenn die Feldstärke gerade 1 V·cm-1
beträgt, wandern die Ionen mit einer Geschwindigkeit von 6 ·
10-4 cm·s-1. Das erscheint uns
sehr langsam, ist es aber nicht, wenn man einen molekularen Maßstab
anlegt, denn in einer Sekunde muss ein Ion etwa 10000 Lösungsmittelmoleküle
passieren.
| Tab.2: Ionenbeweglichkeiten in Wasser bei 298 K, u / 10-4 cm2.s-1.V-1 | |||
| H+ | 36,23 | OH− | 20,64 |
| Na+ | 5,19 | Cl− | 7,91 |
| K+ | 7,62 | Br− | 8,09 |
| Zn2+ | 5,47 | SO42− | 8,29 |
Eine Ausnahme ist das Proton; es ist sehr klein und hat trotzdem eine
sehr hohe molare Leitfähigkeit (Tab. 2). Da nicht einzelne hochsolvatisierte
Protonen durch die Lösung wandern, sondern der Protonen-Transport
erfolgt im wesentlichen durch Umlagerung von Bindungen in einer langen
Kette von (über H-Brücken assoziierten) Wassermolekülen.
Demnach wird die zu beobachtende Leitfähigkeit bestimmt durch die
Schnelligkeit, mit der sich die Wassermoleküle umorientieren können,
um je nach Bedarf in der Lage zu sein, Protonen aufzunehmen oder abzugeben.
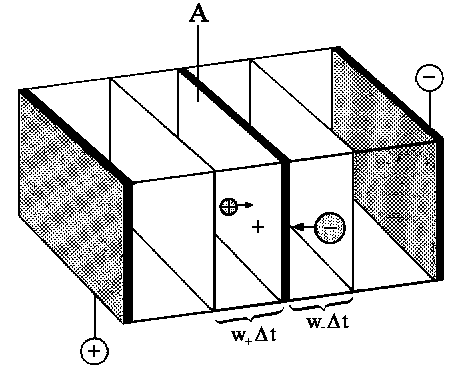 |
| Abb. 2: Alle Kationen, die von A weniger als w+Δt entfernt sind (also in dem Volumen w+AΔt enthalten sind), wandern durch die Fläche A. Die Anionen auf der anderen Seite der gedachten Fläche tragen ebenfalls zum Strom bei. |
Betrachten wir die Lösung eines starken Elektrolyten bei der Konzentration c. Jede Formeleinheit erzeugt ν+ Kationen mit der Ladung z+e und ν− Anionen mit der Ladung z−e (die Teilchendichte einer Ionenart ist deshalb ν+cNA bzw. ν−cNA). Die Anzahl der Kationen, die im Zeitintervall Δt durch ein gedachtes Fenster mit der Fläche A wandern (siehe Abbildung 2), ist gleich der Anzahl der Teilchen, die nicht mehr als w+Δt von diesem Fenster entfernt sind, die also in dem Volumen w+ΔtA enthalten sind. Die Anzahl der Ionen in diesem Volumen ist dann (w+ΔtA) · (ν+cNA). Damit erhalten wir für die Anzahl der Kationen, die in der Zeiteinheit Δt durch ein Fenster mit dem Querschnitt A wandern (das ist der Kationenfluss)
JKationen = (w+ΔtA) .(ν+c NA)/ΔtA = w+ν+cNA
Jedes Kation transportiert die Ladung z+e, der Ladungsfluss wird also
JLadung = z+w+ν+ceNA = z+w+ν+c F
wobei F = e · NA die Faradaysche Konstante
ist. Mit w = uE erhalten wir daraus
| JLadung = z+u+ν+c F E |
Der elektrische Strom durch die Querschnittsfläche A, soweit er von der Wanderung der Kationen herrührt (I+), ist gleich dem Produkt aus dem Ladungsfluss und der Fläche: I+ = J · A. Berücksichtigen wir noch, dass für das elektrische Feld E = U/l gilt, dann folgt für I+
I+ = z+u+ν+c F A U / l
Den Zusammenhang zwischen dem Strom und der Spannung U gibt das Ohmsche
Gesetz, I = U/R an. Der Widerstand
R ist mit der Leitfähigkeit σ über
1/R
= σA/l
verknüpft.
Für Kationen gilt folglich I+ = σ+
U A/l. Vergleicht man das mit der letzen Formel
so ergibt sich σ+ U A/l=
(z+ u+ ν+ c
FAU)/l
| σ+ = z+u+ν+ c F |
Wegen Λm = σ/c
hängt die molare Grenzleitfähigkeit einer Lösung hängt
mit den Beweglichkeiten der einzelnen Ionen über die Beziehung
| Λ0m = {z+u+ν+ + z−u−ν−} F |
zusammen und die molare Ionen-Leitfähigkeit beträgt
| λ+ = z+u+ F |
Entsprechendes gilt für die molare Leitfähigkeit der Anionen:
| λ− = z−u−F |
Für einen symmetrischen z+ : z- Elektrolyten (z.B. CuSO4: z+ = z− = z ; ν+ = ν− = 1) vereinfacht sich das zu
Λ0m = z (u+ + u−) F
Die Hittorfsche Überführungszahl t ist der Bruchteil
des Gesamtstroms, den eine Ionenart transportiert. Enthält eine Lösung
nur zwei Ionenarten, so ist die Überführungszahl der Kationen
bzw. der Anionen:
| t+ = I+/I bzw. t- = I-/I |
Weil der Gesamtstrom I gleich der Summe der Beiträge der Kationen und der Anionen ist, gilt (t++ t−) = 1. Der Beitrag der Kationen zum Gesamtstrom hängt mit der Beweglichkeit der Kationen zusammen ( I+ = z+u+ν+c F A U / l , siehe oben), entsprechendes gilt für die Anionen, und damit erhalten wir für den Zusammenhang zwischen dem Grenzwert (für kleine Konzentrationen c) der Überführungszahl t0 und u die Beziehung
t0+ = z+ν+u+/(z+ν+u+ + z-ν-u−)
Für einen symmetrischen Elektrolyten vereinfacht sie sich zu
t0+ = u+/(u+ + u−) und t0− = u−/(u+ + u−)
Da auch λ+ = z+u+F gilt, erhalten wir:
t0+ = ν+λ+/(ν+λ+ + ν−λ−) und t0− = ν−λ−/(ν+λ+ + ν−λ−)
| ν+λ+ = t0+·Λ0m und ν−λ− = t0−·Λ0m |
Man kann die Überführungszahlen von Ionen direkt messen und damit die Leitfähigkeit λ+, λ− der einzelnen Ionen und ihre Beweglichkeiten u+, u− bestimmen.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.