Gruppen und ihre Darstellungen

Der Begriff der Gruppe

Moleküle (und Kristalle) besitzen in der Regel nicht nur ein sondern mehrere Symmetrieelemente. Dabei ist aber nicht jede beliebige Kombination möglich. Wenn z. B. eine Spiegelebene vorhanden ist, so kann sie nie schräg zu einer Drehachse orientiert sein (die Achse muss entweder senkrecht zur Ebene oder in ihr liegen). Dieses Beispiel macht deutlich, dass die Symmetrieelemente eines Moleküls meist nicht unabhängig voneinander koexistieren, sondern oft miteinander verknüpft sind. Eine Beziehung zwischen ihnen läßt sich über einen der wichtigsten Begriffe der modernen Mathematik den Begriff der Gruppe herstellen. Mögliche Kombinationen ohne Translationssymmetrie nennt man Punktgruppe. Die Bezeichnung bringt zum Ausdruck, dass nur einfache Kombinationen von Symmetrieelementen möglich sind, bei denen es einen ausgezeichneten Punkt oder eine ausgezeichnete Achse gibt, durch welche alle Symmetrieelemente verlaufen.

Die Anzahl (Menge) der Symmetrieelemente, die ein Molekül besitzt, bestimmt dessen Symmetrie, und wird in einer Gruppe zusammengefaßt. Für diese Gruppe ist eine „ Verknüpfungsvorschrift“ definiert, wobei folgende vier Bedingungen erfüllt sein müssen:

  1. Wenn A und B Elemente der derselben Gruppe sind (nicht mit dem Mullikensymbol verwechseln), so ergibt deren Verknüpfung („Multiplikation“ genannt) A · B = C ebenfalls ein Element der Gruppe.

    2. Das „Produkt“ A · B bedeutet hierbei, dass zuerst die Symmetrieoperation B auf das Molekül angewendet wird und dann auf die neue Lage die Operation A. Die Wirkung ist dabei gleich der alleinigen Anwendung der Operation C auf das Molekül. Im allgemeinen ist wegen A · B ¹ B · A das Kommutativgesetz nicht erfüllt.
  2. In jeder Gruppe muss das Einheitselement E einmal vorkommen. E kommutiert mit jedem Element in der Gruppe, z. B. E · B = B · E = B.
  3. Es gilt das assoziative Gesetz: A · B · C = (A · B) · C = A · (B · C)
  4. Zu jedem Element (z.B. A) existiert ein „inverses“ (oder reziprokes), welches ebenfalls in der Gruppe enthalten ist und mit A-1 bezeichnet wird.

    5. Es gilt: A · A-1 = A-1 · A = E.
    Im Falle der Symmetrieoperationen ist die inverse Operation A-1 jene, welche das Molekül in die ursprüngliche Lage (Ausgangsposition) zurückversetzt, aus welcher es durch die Operation A entfernt wurde.
Wenn also diese vier Bedingungen oder Gruppenaxiome erfüllt sind, d.h. die Regel der Verknüpfbarkeit (Multiplikation) gilt, das Assoziativgesetz erfüllt wird, ein Einheitselement existiert und für jedes Element ein dazu inverses Element vorhanden ist, dann stellt die Gesamtheit der Elemente eine Gruppe dar.
Die Anzahl der Elemente einer Gruppe nennt man ihre Ordnung.

Beispiel NH3
Einige der grundlegenden Überlegungen aus der Gruppentheorie sollen im weiteren am Beispiel des Ammoniak-Moleküls näher erläutert werden. Dem Ammoniak-Molekül lassen sich die Symmetrieoperationen E, C3+, C3-, σv, σv' und σv" zuordnen; es gehört demnach zur Gruppe C3v.

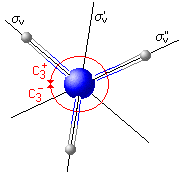
Ammoniak
C3+ - Rotation um die vertikale 3-zählige Drehachse gegen den Uhrzeigersinn
C3- - Rotation um die 3-zählige Drehachse im Uhrzeigersinn (Movie, 455kB)
σv - Spiegelung an vertikaler Ebene σv (Movie, 393kB)
σv' - Spiegelung an vertikaler Ebene σv'
σv"  - Spiegelung an vertikaler Ebene σv"

Wie bereits weiter oben erwähnt, führt die aufeinenderfolgende Ausführung bestimmter Symmetrieoperationen zu weiteren Symmetrieoperationen . Hierzu sei angemerkt, dass die jeweils hintereinander ausgeführten Symmetrieoperationen immer durch eine einzige aus derselben Gruppeersetzbar sind. Diese Tatsache ist eine wesentliche und wichtige Eigenschaft einer jeden Gruppe.
Das Hintereinenderausführen der Operationen wird symbolisch als Multiplikation dargestellt. Die Schreibweise E = C3-C3+ bedeutet, dass zuerst die Rotation gegen den Uhrzeigersinn (C3+) und danach im Uhrzeigersinn (C3-) erfolgt. Vereinbarungsgemäß steht rechts immer die Operation, die zuerst ausgeführt wird. Werden die Faktoren vertauscht (wodurch sich die Abfolge der Symmetrieoperationen ändert) kann es im Unterschied zur gewohnten Schularithmetik vorkommen, das hierdurch das "Produkt" verändert wird. In der nachfolgenden Abbildung wird deutlich, dass die Endposition der Wasserstoffatome im Ammoniak-Molekül davon abhängt, in welcher Reihenfolge die Symmetrieoperationen durchgeführt werden.
 

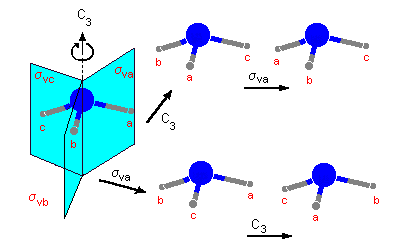Abb.1: Abhängigkeit des Produktes zweier Symmetrieoperationen von der 
Abfolge ihrer Ausführung am Beispiel des Ammoniak-Moleküls.

Aus den sechs Symmetrieoperationen des Ammoniakmoleküls lassen sich durch Multiplikation von jeweils zwei Symmetrieoperationen insgesamt sechsunddreißig Produkte bilden, die in der folgenden sogenannten "Multiplikationstabelle" zusammengefaßt sind (zunächst wird die Transformation aus der Zeile ausgeführt, danach die Transformation aus der Reihe).
 
E 
C3+
C3-
σv
σv' 
σv" 
E 
E 
C3+
C3-
σv
σv' 
σv" 
C3+
C3+
C3-
E 
σv' 
σv" 
σv
C3-
C3-
E 
C3+
σv" 
σv
σv' 
σv
σv
σv" 
σv' 
E 
C3-
C3+
σv'
σv' 
σv
σv" 
C3+
E 
C3-
σv"
σv" 
σv' 
σv
C3-
C3+
E 

Die Transformationen lassen sich auch als Matrizen-Multiplikation darstellen. Allgemeines zur Transformation eines Punktes mit (x,y,z)-Koordinaten gibt's hier.

Durch die Multiplikation zweier Matrizen erhält man eine neue Matrix, die eine Symmetrieoperation darstellt. Beispielsweise stimmt der Ausdruck D(σv)D(C3+) = D(σv")  genau mit der Multiplikationsregel σvC3+ = σv" überein.
Der Satz von sechs Matrizen, die alle Symmetrieoperationen der Gruppe C3v darstellen, heißt Matrix-Darstellung der Gruppe C3v.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.