Ähnlich wie in zweiatomigen Molekülen kann man auch in mehratomigen Molekülen wichtige Informationen über die MO's aus Überlegungen zur Symmetrie des Moleküls sowie zur Symmetrie der an der Bindung beteiligten AO's erhalten. Näherungsweise sind unsere MO's Linearkombinationen aus AO's. Will man die Symmetrie des Problems ausnützen, so konstruiert man zuerst aus den AO's eine Sorte symmetrieadaptierter Linearkombinationen, sogenannte Symmetrie-AO's.
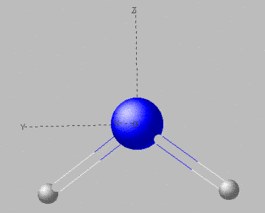
Wir wollen das zunächst an einem Beispiel, dem H2O-Molekül,
erläutern. Wir nehmen an, dass die Struktur gewinkelt ist, mit
zwei gleichen HO-Abständen (die Frage nach der Geometrie beantworten
die Walshschen Regeln). Die Symmetriegruppe des
Moleküls ist dann C2v. Die MO's des H2O müssen
dieser Symmetrie angepaßt sein (symmetrieadaptierte Orbitale), d.h.
sich wie irreduzible Darstellungen der Symmetriegruppe C2v transformieren.
Diese irreduziblen Darstellungen sind bei C2v alle eindimensional;
die Zahlen +1 oder −1 in der Charaktertafel
für C2v geben also an, ob ein MO symmetrisch oder antisymmetrisch
in Bezug auf die Symmetrieoperation der entsprechenden Spalte ist.
| C2v | E | C2 | σv(xz) | σv'(yz) |
| A1 | 1 | 1 | 1 | 1 |
| A2 | 1 | 1 | −1 | −1 |
| B1 | 1 | −1 | 1 | −1 |
| B2 | 1 | −1 | −1 | 1 |
Ein MO der Symmetrie a2 (wir verwenden Kleinbuchstaben für
die Einelektronenzustände, d.h. für die Orbitale, und Großbuchstaben
für den Gesamtelektronenzustand des Moleküls) ist also symmetrisch
bezgl. der Identitätsoperation (E) und bezgl. einer 2-zähligen
Drehung (C2) um die z-Achse (falls eine ausgezeichnete Achse
vorliegt, wird diese immer als z-Achse gewählt) und antisymmetrisch
bezgl. Spiegelung an der xz-Ebene und an der yz-Ebene. Das Kerngerüst
des Moleküls ist invariant gegenüber allen 4 Symmetrieoperationen.
Wir haben dabei noch die Freiheit, die beiden H-Atome in die xz- oder
die yz-Ebene zu legen. Nach der üblichen Konvention wird das Wassermolekül
so orientiert, das alle Atome in der yz-Ebene liegen und die z-Achse
(gleich Hauptdrehachse) die Winkelhalbierende des H-O-H-Winkels bildet.
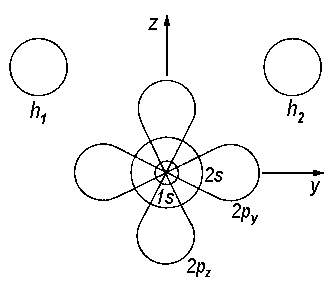 |
| Abb.1: AO's im H2O-Molekül. Das px-Orbital steht senkrecht auf der yz-Molekülebene. |
Es zeigt sich, dass das 1s-AO des O für sich allein in guter Näherung ein MO bildet. Wir wollen deshalb jetzt wie auch später die AO's der inneren Schalen weglassen und uns auf die Valenz-AO's beschränken. Dann können wir in 2s etc. die 2 weglassen und die AO's des Sauerstoffs als s, px, py, pz klassifizieren.
In Bezug auf C2v sind, wie man sich anhand der Charaktertafel klarmachen kann, die AO's des O bereits symmetrieadaptiert. Zur Übung wollen wir dies am Beispiel des px-AOs erörtern. Wir müssen jede der im Kopf der Charaktertafel angegebenen Symmetrieoperationen durchführen und sehen, ob sich bei dieser Operation das Vorzeichen der Wellenfunktion ändert.
Da bei der Identität E keine
Operation durchzuführen ist, bleibt das Vorzeichen der Wellenfunktion
erhalten und wir erhalten in der Spalte für E eine 1:
| E | C2 | σv | σ'v |
|---|---|---|---|
| 1 |
Als nächstes führen wir die Drehung
um 180° um die Hauptdrehachse (z-Achse) durch und sehen, dass
sich das Vorzeichen des px-Orbitals am Sauerstoff ändert.
Wir erhalten also für die Spalte C2 eine -1:
| E | C2 | sv | σ'v |
|---|---|---|---|
|
|
|
Nun führen wir die Spiegelung an der xz-Ebene
durch und erhalten, da sich das Vorzeichen der Atomorbitale nicht ändert
eine 1:
| E | C2 | sv(xz) | σ'v |
|---|---|---|---|
|
|
|
|
Bei der Spiegelung an der yz-Ebene ändert
sich das Vorzeichenmuster und wir erhalten somit eine -1:
| E | C2 | sv | sv'(yz) |
|---|---|---|---|
|
|
|
|
|
Vergleichen wir das Ergebnis unsereer Betrachtungen mit der obigen Charaktertafel für C2v, so erhalten wir für das px-Orbital des Sauerstoffatoms im Wasser das Mullikensymbol b1.
Auf diese Weise erhalten wir die einzelnen AO's zu den irreduziblen
Darstellungen von C2v
| AO | s | px | py | pz |
| irreduzible Darst. | a1 | b1 | b2 | a1 |
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.