Berechnungen mit der Unschärferelation

Aus der Unschärferelation für Energie und Zeit
 

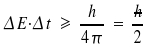erhalten wir, da E = hν:

Es gibt danach eine untere Grenze Δν für die Frequenzschärfe eines Lichtpulses der Länge Δt.

Z.B. kann ein Lichtpuls von 10 ns Dauer nur eine größere Bandbreite als Δν ≥1/4π· 10-8s >> 10 MHz aufweisen. Extrem kurze Lichtpulse im Femtosekundenbereich (1fs = 10-15s) besitzen danach mindestens eine Bandbreite von Δν >>  1014 Hz, was nahezu der Frequenz des sichtbaren Lichtes entspricht, d.h. ein solcher Lichtpuls erscheint uns als weißes Licht.

Wie lang wird ein solcher fs-Puls sein, wenn wir ihn durch einen sehr guten Monochromator mit einer Auflösung von 10 MHz schicken?
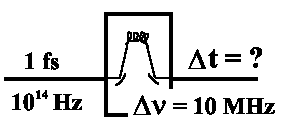
Da dadurch die Frequenz stark spektral eingeengt wird, muss für die zeitliche Länge gelten: Δt  ≥ 1/(4πΔν) ≈ 8·10-9s. D.h. der ursprünglich kurze Puls von 10-15 Sekunden  ist um mehr als sechs Größenordnungen länger geworden!

Wir wollen nun mit der prinzipiellen Unbestimmbarkeit spielen und sie nutzen, um ein Gefühl für die Größe eines Atoms zu bekommen: Wenn wir das Elektron am Wasserstoffatom suchen, dann wird es um Δx = r verschmiert sein. Der Impuls p wird im Bereich p ≈ Δp ≈ h/4πr liegen.

Die kinetische Energie ist

die potentielle Energie

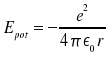
Die Gesamtenergie wäre danach

Für das Minimum der Gesamtenergie ist zu fordern

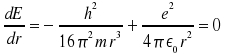  daraus   folgt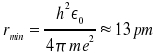

Einsetzen in die Gl. für die Gesamtenergie liefert:

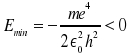
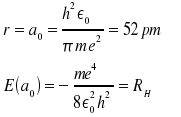Die Energie ist negativ, d.h. das Elektron ist gebunden. Tatsächlich gilt exakt

RH ist die Rydbergkonstante. Wir sind also durch Ausnutzen der Unbestimmtheitsrelation nicht weit von der Wirklichkeit entfernt, denn wir können ungefähr die Größe des H-Atoms und die Ionisationsenergie abschätzen.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.