Konstruktion von Wellenpaketen

Konstruiert man durch Überlagerung mehrerer Wellen mit etwas unterschiedlicher Frequenz bzw. durch ein schmales kontinuierliches Intervall von Frequenzen eine Wellengruppe, so kann man zwei charakteristische Geschwindigkeiten, die Phasen- und die Gruppengeschwindigkeit, unterscheiden. Als einfachstes Modell einer Wellengruppe betrachten wir zunächst die Schwebungsgruppe, die durch Überlagerung zweier Wellen gleicher Ausbreitungsrichtung und Amplitude mit den Kreisfrequenzen ω1 und ω2 entsteht.

Die Wellengruppe wird durch die Funktion

Ψ(x, t)  =  2Ψ0 cos (ω2−ω1/2 t  −  k2−k1/2 x) ei(ω1+ω2/2 t  −  k1+k2/2 x)

beschreiben. Sie läßt sich in zwei Teile zerlegen:

1) ei(ω1+ω2/2 t  −  k1+k2/2 x)   entspricht einer ebenen, in x-Richtung unendlich ausgedehnten Welle mit der mittleren Kreisfrequenz <ω> = ω2+ω1/2 und dem mittleren Wellenvektor <k> =  k2+k1/2. Die Phasengeschwindigkeit vph wird dabei definiert als

vph  =  <ω>/<k>

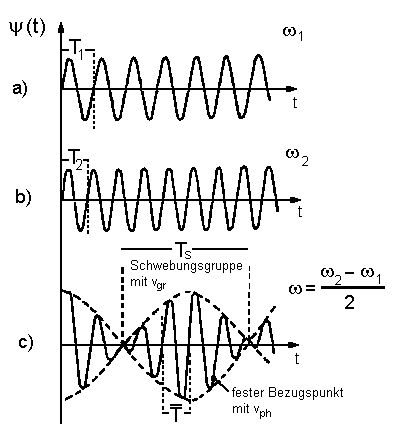Abb.1: Einfaches Beispiel für eine Wellengruppe: Überlagerung (c) zweier Wellen mit den Kreisfrequenzen ω1 (a) und ω2 (b) bzw. mit den Wellenvektoren k1 und k2 mit zeitabhängigen Amplituden bei x = const. 

Sie ist anschaulich die Geschwindigkeit eines festen Bezugspunktes auf der Welle von konstanter Phase: Man setzt sich z.B. auf einen "Wellenberg" und beobachtet dessen Ausbreitungsgeschwindigkeit.

2) Die Amplitudenfunktion

2Ψ0 cos (ω2−ω1/2 t  −  k2−k1/2 x)

entspricht der Hüllkurve in Abbildung 1. Für das Maximum der Amplitudenfunktion ist das Argument der cos-Funktion 0 oder ein Vielfaches von π:

ω2−ω1/2 t  −  k2−k1/2 x  =  0

Daraus erhält man die Gruppengeschwindigkeit:

vgr  =  x/t  =  ω2−ω1/k2-k1  =  Δω/Δk

Für ein Wellenpaket, bestehend aus einem schmalen kontinuierlichen Spektrum von Frequenzen, gilt die allgemeine Beziehung:

vgr  =  dω/dk  =  d(hω)/d(hk)  =  dE/dp  = d(p²/2m)/dp  =  vTeilchen

Bei dieser Ableitung wurde die nichtrelativistische kinetische Energie des Teilchens verwendet. Dies gilt für Teilchen mit c << c.

Dispersion liegt dan vor, wenn der Zusammenhang zwischen ω und k nichtlinear ist und sich vph und vgr dadurch unterscheiden.
 
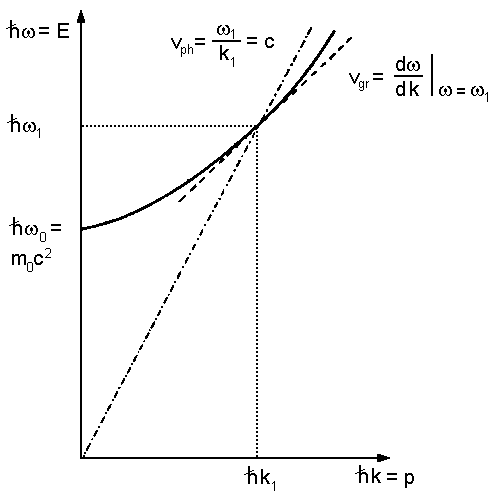Abb.2: Gruppengeschwindigkeit vgr und Phasengeschwindigkeit vph für Materieteilchen (dicke Linie) im Vergleich zu Photonen (strichpunktierte Linie) mit vgr = vph = c im Diagramm Energie hω (mit der Kreisfrequenz ω) gegen Impuls hk (mit der Wellenzahl k). E0 = m0c² ist die Nullpunktsenergie von Materieteilchen, die in dieser Abbildung stark verkleinert dargestellt wurde: Normalerweise würde die Phasengeschwindigkeit einen nahezu senkrechten Verlauf zeigen. Die Werte hω1 bzw. hk1 sind für beide (Teilchen und Welle) gleich, ebenso die Phasengeschwindigkeiten, nicht jedoch die Gruppengeschwindigkeiten.
In Abbildung 2 ist als Beispiel der Dispersion die Funktion E(p) (entspricht der häufig verwendeten Funktion ω(k)) für Materieteilchen im Vergleich zu Photonen gezeigt. Für erstere gilt E = p²/2m + E0, d.h. ω ~ k².

Man kann daraus erkennen, dass vph > vgr ist. Dies ist allgemein für Materieteilchen gültig. Der Zusammenhang von ω und k für Photonen im Vakuum ist linear. Dies läßt sich aus der Beziehung

c  =  λ ·ν  =  2π/k· ω/2π  =  const.

erkennen. Es tritt also keine Dispersion auf, und vph = vgr.

Die Bedeutung der Dispersion ist für den räumlichen und zeitlichen Verlauf eines Wellenpakets mit gaußförmiger Orts- (und damit auch Impuls-) Verteilung der Intensitäten ist in Abbildung 3 gezeigt.
 
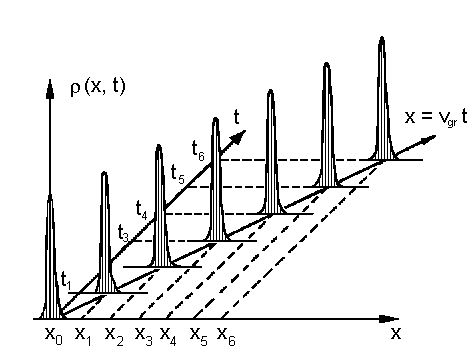
a) lineare Dispersionsrelation (ω ~ k)
b) quadratische Dispersionsrelation (ω ~ k²)
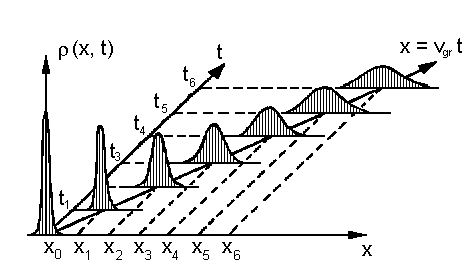Abb.3: Räumlicher und zeitlicher Verlauf der Intensität r(x,t) = Ψ2 (x,t) eines Wellenpaketes mit gaußförmiger Orts- und damit auch gaußförmiger Impulsverteilung für (a) lineare Dispersion (z.B. Photonen im Vakuum) und (b) quadratischen Dispersion (z.B. Elektronen oder Photonen in Glas).
Man sieht, dass bei quadratischer Dispersion die Wellen mit zunehmender Zeit räumlich auseinanderlaufen. Dies gilt nicht nur für Materieteilchen, sondern auch für Photonen in einem Medium mit freuquenzabhängigem Brechungsindex und damit Lichtgeschwindigkeit.

Den Schlüssel zum Verständis des Dualismus Welle-Teilchen liefert sie Wahrscheinlichkeit: Das Maximum des Wellenpaketes ist nicht mit dem klassisch exakt definierten Ort des Matrieteilchens zu identifizieren, sondern lediglich die Stelle, an der man bei einem Experiment mit vielen Teilchen (Teilchenstrahl) Teilchen mit der größten Wahrscheinlichkeit findet. Die analoge Aussage für die Verteilung des Impulses im k-Raum lautet: Die Welle k mit der größten Amplitude F(k) entspricht dem Impuls hk, der sich bei einer Impulsmessung mt der größten Wahrscheinlichkeit ergibt. Genauer gesagt, ist die Wahrscheinlichkeit für das Auffinden eines bestimmten Wertes proportional zum Amplitudenquadrat der Welle.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.