Newton beschrieb noch Licht ganz im Sinne seiner
mechanistischen Weltbeschreibung als Teilchen (Quanten). Doch schon im
17. Jahrhundert führte Christiaan
Huygens Elementarwellen ein, um das Verhalten von Licht zu beschreiben.
Die Wellennatur des Lichtes wurde durch das bahnbrechende Beugungsexperimente
am Doppelspalt von Thomas Young
1801 endgültig in die Lehrmeinung eingeführt und niemand zweifelte
mehr an der Wellennatur des Lichtes, denn alle Phänomene konnten dadurch
richtig erklärt und quantitativ korrekt beschrieben werden. Plancks
Theorie des Schwarzen Körpers war eine extrem gewagte Theorie, die
zwar dieses eine Phänomen richtig beschrieb, doch insgesamt durch
die Einführung von Quanten mehr Probleme als Lösungen aufwarf.
Doch bald wurden andere Experimente durchgeführt und die Ergebnisse
konnten erst erklärt werden, wenn man Quanten einführte. Im Grunde
wurde dadurch alles noch verwirrender, denn mal verhielt sich das Licht
wie eine Welle, mal wie ein Teilchen (Lichtquant). Doch zunächst zu
den beiden Experimenten, die am deutlichsten den Teilchencharakter des
Lichts untermauern: Der photoelektrische Effekt und
der Compton-Effekt:
 |
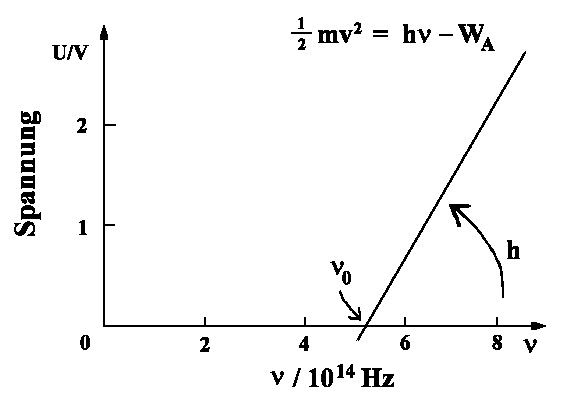 |
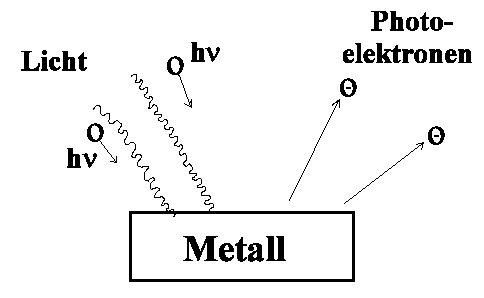
Trifft elektromagnetische Strahlung (neudeutsch für Licht) einer hinreichend
hohen Frequenz auf die Oberfläche eines Metalls, dann werden Elektronen
ausgelöst, die man (konsequent) Photoelektronen nennt. Dies
ist der photoelektrische Effekt.
klassische Erklärung:
Das elektromagnetische Feld E
der einfallenden Lichtwelle übt eine hin und her schwingende Kraft
auf die freien Elektronen im Metall aus. Daraus folgt, dass mit zunehmender
Amplitude (nicht Frequenz) Elektronen austreten. Dies steht im Gegensatz
zum
Experiment:
Es treten keine Photoelektronen unterhalb einer Frequenz
νo
auf.
Die Geschwindigkeit der Elektronen ist unabhängig von der Lichtleistung.
Die Photoelektronen treten auch bei schwacher Lichtleistung sofort
aus.
Quantenerklärung:
Ein Energiequant hν wird absorbiert. Da
das Elektron im Metall gebunden ist, wird ein Teil der Energie benötigt,
um Austrittsarbeit WA zu leisten. Der Rest der Energie
wird als kinetische Energie frei.
| ½ me v2 = hν - WA |
Analogie Fußball:
Ein Fußball der Masse m wird auf eine Anhöhe H getreten.
Der Tritt verleiht dem Ball zunächst eine bestimmte Energie E, die
analog zu hν beim Photoeffekt ist. Wenn der
Ball die Anhöhe emporgerollt ist, gewinnt er potentielle Energie mgH,
analog zur Austrittsarbeit WA. Die Geschwindigkeit v des Balles
auf der Anhöhe ist daher über
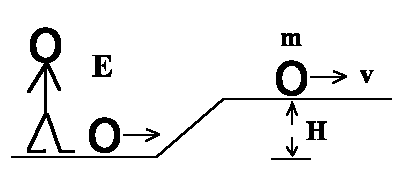 |
| ½ m v2 = E − mgH |
Der Compton-Effekt ist der deutlichste Beleg für die Existenz von
Teilchen als Träger der elektromagnetischen Strahlung.
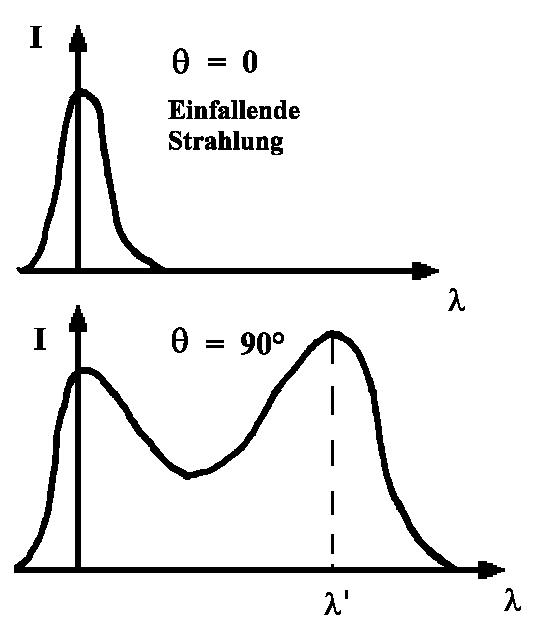 |
Experiment:
Röntgenstrahlen fallen auf Graphit und werden z.T. in alle Richtungen
gestreut. Die Streustrahlung besitzt eine Komponente mit genau der gleichen
Frequenz wie die einfallende Strahlung, während die andere Komponente
eine niedrigere Frequenz aufweist. Die Frequenz nimmt um so mehr ab, je
größer der Streuwinkel θ wird.
Energieerhaltung:
Energie vor dem Stoß = Energie nach dem Stoß :
hν + m0c2 = hν’ + mc2
hν − hν’ = mc2 − m0c2
ν -ν' = m0c²/h{[1/(1 − v²/c²)½]− 1}
wobei die Einsteinsche Beziehung m = mo/(1
- v²/c²)½
benutzt wurde.
Das Photon gibt also Energie auf das Elektron ab und die Frequenz
verringert sich (ν’< ν).
Impulserhaltung:
Ein Photon besitzt einen Impuls; denn nach Einstein ist
E = mc2 = p · c = hν = hc/λ
| p = h/l p = hν/c |
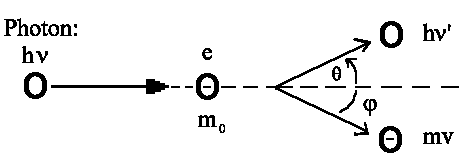 |
Impuls p = h/cν' | ; px = h/cν' · cosθ |
| Impuls p = m · v | ; px = m · v · cosj |
1/ν' = 1/ν + h/m0c²(1 − cosθ)
| λ' = λ + h/moc (1 - cosθ) |
Dir Größe h/moc wird Comptonwellenlänge genannt und hat den Wert 0,00243 nm.
Die maximale Wellenlängenverschiebung tritt für θ = 180° (Rückwärtsstreuung) auf.
Dlmax = λ' - l = 0,00486 nm (unabhängig von der Wellenlänge)
| Klassisch gibt es keine Wellenlängenverschiebung, da h = 0 ! |
Vorhersagen werden durch das Experiment bestätigt:
Die Quintessenz all dieser Experimente: Photonen verhalten sich wie Teilchen !
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.