Das Unvermögen exakt zu wissen, wie schnell etwas wo ist (Unschärferelation)

Wenn die Materie wirklich Teilchen- und Wellencharakter aufweist, was hat das dann für die gleichzeitige Messung von Ort und Geschwindigkeit, d.h. Impuls, zur Folge? (Man denke an die klassische Beschreibung bei der immer Ort und Impuls zu jedem Zeitpunkt festgelegt sind).

Wenn wir ein Teilchen durch einen Spalt schicken, dann können wir den Ort bis auf die Breite Δx des Spaltes genau festlegen. Je kleiner wir Δx machen, um so genauer wissen wir, wo sich das Teilchen befindet.

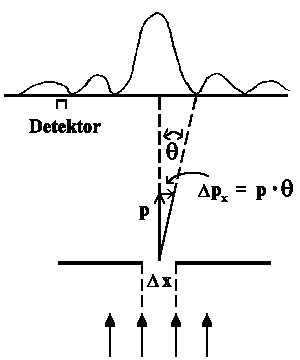
Das erste Minimum tritt auf, wenn θ = λ/Δx (Interferenzbedingung) ist. (Die Wellen von der einen Kante legen eine Wellenlänge λ mehr zurück als die Wellen von der anderen Kante des Spalts). Der Impuls des Photons in x-Richtung ist:

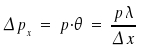
Da p = h/λ ist, erhalten wir


Heisenberg kam gleichen Ergebnis, indem er sich gedanklich ein Elektron unter einem Mikroskop "ansah":

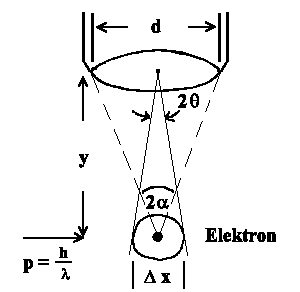Man sieht nur Licht, dass vom Elektron gestreut wird und im Winkel von 2α auf die Linse fällt.

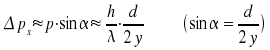
Die genaue Position des Elektrons ist aufgrund der Beugung des Lichtes am Objektiv nicht genau bekannt (begrenztes Auflösungsvermögen).


Anmerkung:
Es wurde der „größte Fehler“ angesetzt; z.B. wurde bis zum ersten Minimum bei der Beugung am Spalt gegangen. Setzt man besser den statistischen Fehler einer (optimalen) Verteilung ein, dann erhält man, wie später gezeigt wird, die

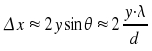
Heisenbergsche Unschärferelation 

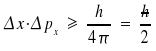
Die Größe h (gesprochen h quer; der Querstrich liegt eigentlich höher, doch das html-Format erzwingt diese Schreibweise) ist lediglich eine kürzere Schreibweise, um den häufig auftretenden und daher lästigen Faktor 2π loszuwerden. Die Relation Δx · Δp ≥ h/2 erreicht man für optimale Verläufe (Gauß) von x und p.
 

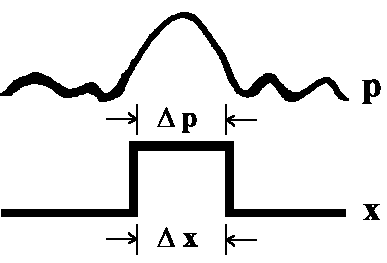
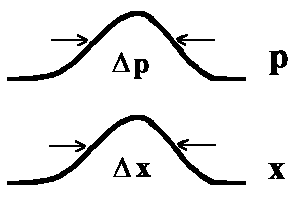
Spalt Gauß'scher Verlauf

Man könnte nun einwenden, dass wir den Impuls und den Ort eines Photons sehr wohl wissen können, denn beim Spaltexperiment kann ich den Spalt Δx beliebig klein machen und nun brauche ich auf dem Schirm nur nachsehen, wo das Teilchen (Photon) auftrifft. Die Ablenkung des Teilchens von der ursprünglichen Richtung gibt die Impulsänderung an.
 

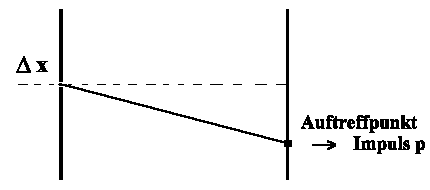In diesem Fall kenne ich jedoch nur den Ort x zu einem Zeitpunkt und den Impuls p zu einem anderen (hier späteren) Zeitpunkt. Die Unbestimmtheitsrelation ist jedoch eine Aussage über die Möglichkeit gegenwärtiger, gleichzeitiger Kenntnis von Ort und Impuls und damit die Möglichkeit der Vorhersagbarkeit; nicht dagegen über das was war, bevor die gegenwärtige Messung durchgeführt wurde.

Sie ist nicht Ausdruck experimenteller Unzulänglichkeit, sondern ein quantitativer Ausdruck der Messbarkeit überhaupt. Das Unbestimmtheitsprinzip beruht darauf, dass mit jeder Messung eine Störung des Systems grundsätzlich einhergeht, die prinzipiell nicht genau bestimmbar ist.
Man darf nur Begriffe verwenden und mitteilen, die durch irgendeine Messvorschrift angegeben werden können. Wir können den Ort und den Impuls exakt messen. Beides zugleich jedoch nur in einem gewissen Rahmen, der durch die Unbestimmbarkeitsrelation gegeben ist.

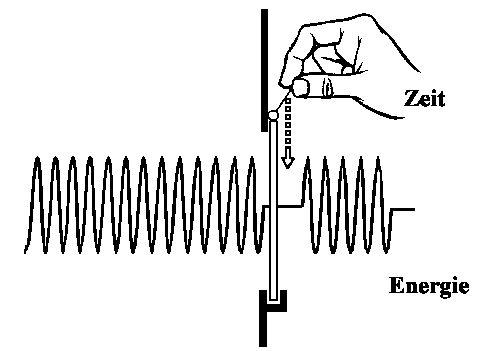
Nicht nur zwischen p und x, d. h. Impuls und Ort, gibt es eine Unbestimmtheitsrelation, sondern auch zwischen anderen Größen, wie Energie und Zeit:

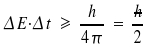da E = hν

Es gibt danach eine untere Grenze für die Frequenzschärfe eines Lichtpulses.


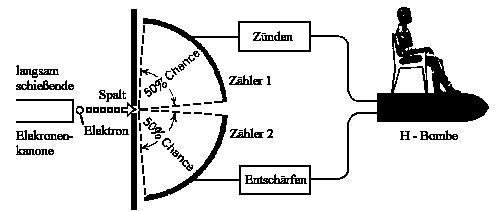
Die Unschärferelation lehrt uns, dass es prinzipiell keine Möglichkeit gibt vorherzusagen, ob ein Elektron (in der unteren Abbildung) die H-Bombe zündet oder entschärft!
 


 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.