Komplexe Zahlen und Funktionen

Der Zahlenbereich der reellen Zahlen, in desse Rahmen z. B. die Wurzel
aus einer negativen Zahl nicht definiert ist, kann erweitert werden auf
die komplexen Zahlen. Eine komplexe Zahl c kann wie ein Vektor als geordnetes
Paar (a, b) beschieben werden, wobei a dem Realteil entspricht ((a, 0)
ist eine rein reelle Zahl) und b dem Imaginärteil ((0, b) ist eine
rein imaginäre Zahl). Dargestellt werden komplexe Zahlen häufig
durch
c = Re c + iIm c = a + ib
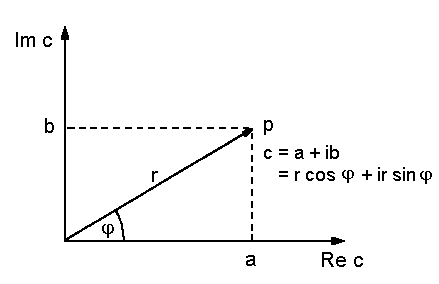 |
| Abb. 1: Komplexe Zahlen, dargestellt in der
Gaußchen Zahlenebene |
Aus Abbildung 1 kann man erkennen, dass c auch durch Angabe der Größen
r (= Länge des Ortsvektors zum Punkt P, Betrag der komplexen Zahl
c) und des Winkels j eindeutig festgelegt ist.
Für die Umrechnung gilt die sog. Eulersche Formel:
c = a + ib = r (cos j
+ i sin j) = r ·
eij
mit r² = a² + b² und tan j =
b/a.
Wichtige Rechenregeln:
-
Addition (Subtraktion analog mit Minuszeichen)
c1 + c2 = (a1 + a2,
b1 + b2) = (a1 + a2)
+ i(b1 + b2)
-
Multiplikation
c1 · c2 = r1eij1
− r2eij2
= (r1 · r2) ei(j1
+ j2)
-
Division
c1/c2
= r1/r2
ei(j1 −
j2)
-
Potenz
cn = rn eijn
-
Konjugiert komplexe Zahl c*
c* = a − ib = re−ij
-
Betrag
Ö(|c|²)
= Ö(cc*)
= Ö(reij
re−ij)
= r
-
Polardarstellung
i = eiπ/2
mit i² = −1
Die komplexe Zahlendarstellung wird z.B. angewendet, um Phasenverschiebungen
zwischen Wechselströmen und -spannungen (über komplexe Widerstände
= Impedenzen) oder zwischen anregendem elektrischen Wechselfeld und
induzierter Polarisation (über komplexe Dielektrizitätskonstanten)
zu beschreiben. Ganz allgemein wird die komplexe Schreibweise häufig
für die Beschreibung periodischer Vorgänge über e-Funktionen
verwendet, wobei die Eulersche Formel zur Umrechnung in Real- und Imaginärteil
der Amplituden dient.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
