Seltsame Klammern und Wellenfunktionen

Wir wollen nun die Beobachtungen beim Doppelspalt-Experiment, d.h. "Welcher-Weg"-Information mathematisch beschreiben. Das Doppelspalt-Experiment zeigt uns, dass die Gesamtwahrscheinlichkeitsamplitude über der Summe der Einzelamplituden für die beiden Wege 1 und 2 gegeben ist.

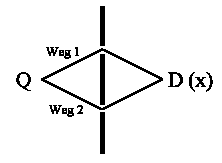Schreiben wir dies etwas präziser: Die Amplitude für den Weg 1 setzt sich zusammen aus einem Teilweg von der Quelle Q bis zum Spalt 1 und aus einem weiteren Teilweg vom Spalt 1 bis zum Detektor D am Ort x. Wir kennzeichnen jeden Weg durch spitze Klammern der Form

Die Gesamtwahrscheinlichkeitsamplitude von Q über den Weg 1 und den Weg 2 nach dem Ort x zu gelangen ist dann:

<x|Q> = <x|1><1|Q> + <x|2><2|Q>

Man erkennt, wie einfach es nun geworden ist, die Gesamtwahrscheinlichkeitsamplitude anzugeben, wenn es beliebig viele Spalte gibt:

<x|Q> = Σ_i=1<x|i><i|Q>

Man muss nur die einzelnen Wege i aufsummieren.

Aus dieser Beziehung kann man auch ablesen, dass die rechte Seite der Gleichung der linken Seite entspricht, wenn man Σ_i=1 |i><i| durch den senkrechten Strich | ersetzt.Oder etwas mathematischer, wenn

Σ_i=1 |i><i| = 1

gilt. Dies ist im Augenblick natürlich nur eine nette mathematische Schreibweise. Sie besagt, dass alles "vollständig" ist, wenn kein Weg vergessen wird. Dadurch, dass die Summe 1 ist, kann man natürlich immer so eine 1 in mathematische Ausdrücke "reinschieben", ohne dass sich etwas an der Beschreibung ändert. Warum sollte man dann eine 1 reinschieben, wenn sich sowieso nichts ändert? Nun, häufig lassen sich die <x|1>, <x|2>, .... leichter berechnen als <x|Q>.

Die Größe <1|Q>, bzw. <2|Q>, gibt den Anteil der Quelle Q an, die über den Spalt 1 bzw. über den Spalt 2 zur Wahrscheinlichkeitsamplitude beitragen. Wir können diese Anteile abkürzen mit a₁ = <1|Q> und a₂ = <2|Q>. Falls in unserem Beispiel die Quelle Q genau in der Mitte zwischen den beiden Spalten liegt, dann sind natürlich a₁ und a₂ gleich groß (a₁ = a₂) und die Gesamtwahrscheinlichkeitsamplitude <x|Q> ist proportional zu <x|1> + <x|2>. Schreiben wir für <x|1>ºf₁(x), <x|2>ºf₂(x) und für <x|Q>ºy(x), dann erhalten wir das uns bereits bekannte Ergebnis y(x) ~f₁(x) + φ₂(x).

Für den allgemeinen Fall erhalten wir die zwei äquivalenten Schreibweisen

<x|Q> = a₁<x|1> + a₂ <x|2>

y(x) = a₁φ₁(x) + a₂φ₂(x)

Die Funktionen y(x) und φ(x) in der rechten Schreibweise nennt man Wellenfunktionen. Die linke Schreibweise geht auf Paul Dirac zurück und hat den Vorteil, dass man das "x" auch weglassen kann:

|Q> = a₁ |1> + a₂ |2>

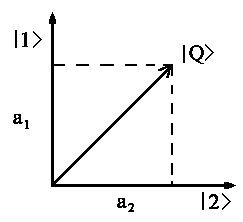Diese Gleichung ist wie ein Vektor |Q>, der nach zwei Einheitsvektoren |1> und |2> zerlegt werden kann, wobei die Projektion von |Q> auf die Richtung |1> die Länge a₁ hat und die Projektion auf die Richtung |2> die Länge a₂ ergibt. Genannt wird die "linke" Klammer <| bra Vektor und die "rechte" Klammer |>ket Vektor. Zusammen gesetzt bra(c)ket, was im Englischen Klammer heißt

Interessiert uns nicht der Ort x, sondern beispielsweise der Impuls p, dann "multiplizieren" wir einfach von links mit <p| und erhalten so die Wahrscheinlichkeitsamplitude für den Impuls p eines Teilchens, das von der Quelle Q stammt:

<p|Q> = a₁<p|1> + a₂<p|2>

Nun messen wir, welchen Weg das Teilchen nimmt. Kommt es bespielsweise über den Weg 1; dann ist die Gesamtwahrscheinlichkeitsamplitude:

<x|Q> = a₁<x|1> y(x) = a₁φ₁(x)

und die Wahrscheinlichkeit, es am Ort x zu beobachten ist:

P₁(x) = |a₁|² · |<x|1>|²

P₁(x) = |y(x)|² = |a₁|² |φ₁(x)|²

Um das Betragsquadrat zu bilden, müssten wir einfach die Wahrscheinlichkeitsamplitude mit dem konjugierten Wert multiplizieren (z.B.: |1 + 2i|² = (1+2i)(1−2i) = 1−(2i)² = 5). Für das konjugiert Komplexe in der Dirac'schen Schreibweise drehen wir einfach die Klammern um: (<x|1>)* = <1|x>.
P(x) ist die Wahrscheinlichkeit das Teilchen am Ort x zu treffen. Wenn ich nun das Teilchen hinter dem Spalt registriere, egal wo es auftrifft, dann muss sicherlich gelten:

P₁ = |a₁|²

denn a₁ gibt ja gerade den Anteil der Wahrscheinlichkeitsamplitude an, der über den Spalt 1 verläuft. Folglich muss gelten:

P₁ = _-∞ò^¥P(x)dx = |a₁|² Σ_x |<x|1>|² = |a₁|²

Σ_x <1|x> <x|1> = 1

<1|1> = 1, da Σ_x |x><x| = 1

P₁ = _-∞ò^¥P(x)dx = |a₁|² ò|f₁(x)|²dx = |a₁|²

_-∞ò^¥ |φ₁(x)|²dx = 1

In der Dirac'schen Schreibweise erkennen wir wieder, dass eine vollständige Summation über alle Werte von x die Identität 1 ergibt. Der Ausdruck <1|1> = 1, bzw. ò|f₁(x)|²dx = 1 bringt anschaulich zum Ausdruck, dass das Teilchen nicht verschwinden kann, sondern irgendwo sein muss.

Was wir gerade abgeleitet haben, gilt für ein Teilchen, das wir beobachten, wenn es den Weg 1 nimmt. Entsprechend gilt natürlich, wenn wir feststellen, dass es den Weg 2 nimmt:

P₂ = |a₂|² <2|2> = 1, bzw. _-∞ò^¥ |φ₂(x)|²dx = 1

Die Gesamtwahrscheinlichkeit P, dass es entweder den Weg 1 (mit der Wahrscheinlichkeit P₁) oder den Weg 2 (mit der Wahrscheinlichkeit P₂) geht und irgendwo ankommt, muss gleich eins sein, denn wir betrachten ja nur solche Teilchen, die entweder über Weg 1 oder über Weg 2 gehen. Folglich gilt: P₁ + P₂ = 1

P₁ + P₂ = 1

|a₁|² + |a₂|² = 1

Wir können auch dieses Ergebnis für beliebig viele Wege verallgemeinern und erhalten:

Σ_i |a_i|² = 1

<i|i> = 1 _-∞ò^¥ |φ_i(x)|²dx = 1

Die Koeffizienten a_i sagen uns, wie groß die Beiträge der einzelnen Spalte ist. Stellen wir uns nun ein "Dreispaltexperiment" vor, bei dem der dritte Spalt relativ weit von den beiden ersten entfernt ist. Uns ist anschaulich klar, dass dieser dritte Spalt nur wenig zu unserer Intensitätsverteilung (insbesondere in Richtung hinter den beiden anderen Spalten) beitragen wird. D.h. wir könnten unser System näherungsweise durch a₁<x|1> + a₂<x|2> beschreiben, da der dritte Summand a₃<x|3> aufgrund der Kleinheit von a₃ nur unwesentlich zur Summe beiträgt. Allerdings muss man beachten, dass für die Wahrscheinlichkeiten die Quadrate eingehen, jedoch nicht für die Amplituden. Z.B. könnten wir messen, dass jeweils 49% aller Teilchen über Weg 1 und Weg 2 gehen und nur 2% über Weg 3 (49% + 49% + 2% = 100%), d.h. der Anteil ^Weg
3/_{Weg 1} beträgt lediglich ²/₄₉≈ 0,04. Der Anteil an der Wahrscheinlichkeitsamplitude liegt jedoch bei |a₃|/|a₁| ≈ 0,2, denn es ist |a₁| = |a₂| = 0,7 und |a₃| ≈ 0,14.

Nun machen wir das Doppelspalt-Experiment, ohne zu beobachten durch welchen Spalt das Teilchen geht. Für die Wahrscheinlichkeit es am Ort x zu finden gilt dann:

P(x) = \|<x\|Q>\|² <x\|Q> = a₁<x\|1> + a₂<x\|2>	P(x) = \|y(x)\|² y(x) = a₁φ₁(x) + a₂φ₂(x)
P(x) = \|a₁\|²\|<x\|1>\|²+\|a₂\|²\|<x\|2>\|² + a₁a₂<1\|x><x\|2> + a₁a₂<2\|x><x\|1>	P(x) = \|a₁\|²\|φ₁\|²+\|a₂\|²\|φ₂\|²+a₁a₂φ₁φ₂ + a₁a₂φ₁φ₂

Die beiden ersten Summanden sind identisch mit der Wahrscheinlichkeit, die man erhält, wenn man beobachtet, durch welchen Spalt das Teilchen kommt. Die beiden letzten Summanden sorgen für das Interferenzverhalten, d.h. Auslöschung bzw. Verstärkung der Intensität.

Die Gesamtwahrscheinlichkeit das Teilchen nach Passieren des Doppelspaltes irgendwo zu finden muss eins sein, denn das Teilchen darf sich ja nicht ins Nirwana verflüchtigen. Also muss gelten:

1 = |a₁|²∫|φ₁|²dx + |a₂|²∫|φ₂|²dx + a₁*a₂òf₁*φ₂dx + a₁a₂*òf₁φ₂*dx

Da ∫|φ₁|²dx = ∫|φ₂|²dx = 1 und |a₁|² + |a₂|² = 1 gilt, folgt daraus

_-∞∫^+∞φ₁*φ₂dx = _-∞∫^+∞φ₁φ₂*dx = 0

In der Dirac'schen Schreibweise bedeutet das:

<1|2> = <2|1> = 0

Wir können die Ergebnisse auch so zusammenfassen, dass für beliebig viele Wege allgemein gilt:

_-∞∫^+∞φ_i*φ_kdx = δ_i,k

<i|k> = δ_i,k

d_i,k = _{

1 für i = k

0 für i ¹ k

Man spricht von orthonormalen Zuständen, in Analogie zur Vektorrechnung bei der die auf eins normierten Einheitsvektoren i und k senkrecht aufeinander stehen:

i · k	= _{	1 für i = k
		0 für i ¹ k

Falls die Zustände nicht auf eins normiert sind (was ja nur nötig ist, um sagen zu können, die Gesamtwahrscheinlichkeit sei eins), dann spricht man von orthogonalen Zuständen (im Gegensatz zu orthonormalen Zustände, die zusätzlich auf eins normiert sind). Orthogonale Zustände hat man immer, wenn sie sich nicht gegenseitig beeinflussen.
Der Begriff orthogonal verwirrt vielleicht etwas. Zur Verdeutlichung kann man nachrechnen, dass die Funktionen
φ₁(x) = (¹/₂)^½, φ₂(x) = (³/₂)^½x und φ₃(x) = (⁵/₈)^½(3x²-1)
im Intervall [-1,+1] orthonormal sind, d.h. die Integrale ₋₁∫¹φ_i(x)φ_k(x)dx liefern den Wert 1 wenn i = k ist und sonst 0.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.

P(x) = \|<x\|Q>\|² <x\|Q> = a₁<x\|1> + a₂<x\|2>	P(x) = \|y(x)\|² y(x) = a₁φ₁(x) + a₂φ₂(x)
P(x) = \|a₁\|²\|<x\|1>\|²+\|a₂\|²\|<x\|2>\|² + a₁a₂<1\|x><x\|2> + a₁a₂<2\|x><x\|1>	P(x) = \|a₁\|²\|φ₁\|²+\|a₂\|²\|φ₂\|²+a₁a₂φ₁φ₂ + a₁a₂φ₁φ₂