Der Tunneleffekt (Herleitung)

Der Tunneleffekt - Eine Herleitung

Ein Teilchen der Masse m fliegt mit der Energie E von links auf die Potentialbarriere der Höhe V und Breite a. Die Schrödingergleichung zerfällt in drei Gleichngen, die für jeweils eine der drei Zonen gelten:

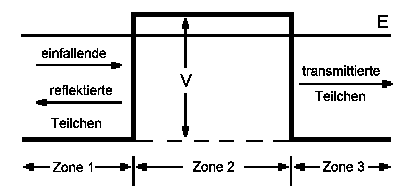
Zone 1

Zone 2

Zone 3

^h²/_2m^d²/_dx²y₁ + Ey₁ = 0

y₁ = A₁e^ik1^x + B₁e^−ik1^x

k₁² = 2m ^E/_h²

^h²/_2m^d²/_dx²y₂+(E -V)y₂ = 0

y₂ = A₂ e^ik2^x + B₂ e^−ik2^x

k₂² = 2m ^(E−V)/_h²

^h²/_2m^d²/_dx²y₃ + Ey₃ = 0

y₃ = A₃ e^ik3^x + B₃ e^−ik3^x

k₃² = k₁² = 2m ^E/_h²

Falls die Energie E des Teilchens kleiner als V ist, dann ist in Zone 2: k₂²< 0, d.h. k₂ ist imaginär. Schreiben wir daher k₂ = ik, wobei k nun die reale Größe k²= 2m ^(V−E)/_h² darstellt, dann erhalten wir für die Wellenfunktion in Zone 2:

y₂ = A₂ e^−k^x + B₂ e^kx

Diese Funktion oszilliert nicht, sondern zeigt nur eine exponentielle x-Abhängigkeit.

Wir müssen nun die Koeffzienten A_i und B_i (i = 1, 2, 3) bestimmen. Da die Teilchen von links einfallen, muss der Koeffizient B₃ Null sein, da die Wellenfunktion B₃ e⁻ⁱ^k1^x für Teilchen gilt, die von rechts nach links fliegen. Diese Teilchen gibt es aber nicht ! Der Koeffizient B₁ muss nicht null sein, da Teilchen am Potential reflektiert werden können und sich dann nach links fortbewegen. Die verbleibenden Koeffizienten werden über die Randbedingungen und die Normierung festgelegt: y und y' müssen stetig sein, d.h. es muss gelten für

	x = 0	x = a
y stetig:	A₁ + B₁ = A₂ + B₂	A₂ e^−k^a + B₂ e^k^a = A₃ e^ik1^a
y' stetig:	ik₁A₁ − ik₁B₁ = −kA₂ + kB₂	-kA₂ e^−k^a + kB₂ e^ka = ik₁A₃ e^ik1^a

Der Koeffizient B₁ bestimmt die Wahrscheinlichkeit (über |B₁|²), dass das Teilchen reflektiert wird und der Koeffizient A₃ bestimmt die Wahrscheinlichkeit (über |A₃|²), dass das Teilchen die Barriere V durchdringt und sich dann auf der rechten Seite mit hk fortbewegt. Die Transmissionswahrscheinlichkeit T = |A₃|²/|A₁|² gibt die Chance an, dass das Teilchen von links kommt und auf der rechten Seite der Bariiere fortfliegt. Einfache, aber umständliche Umformungen der obigen Randbedingungen ergeben:

T = {1 + [e^k^a− e^−k^a]²_/[16 ^E/_V (1-^E/_V)]}^-1 mit k = (^2m(V-E)/_h²)^½

oder T = {1 + sinh²(ka)_/[4 ^E/_V (1-^E/_V)]}^-1

Offensichtlich ist T ungleich Null, obwohl E < V ist, d.h. das Teilchen tunnelt durch die Potentialbarriere, was klassisch verboten ist.
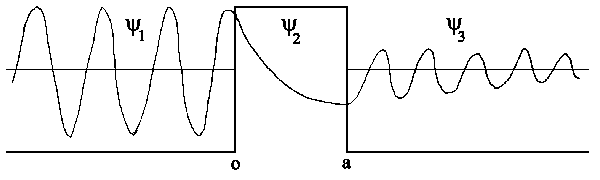
Die Wellenfunktion fällt an der Stelle x = 0 nicht abrupt auf Null, da V nicht unendlich hoch und breit ist.
Näherungsweise gilt für ka>1:

T ≈ 16 ^E/_V(1 − ^E/_V) e^−2ka

Für E > V kann T < 1 sein, d.h. Teilchen werden reflektiert, obwohl ihre Energie ausreicht, das Potential zu überwinden. Hier gilt (k' = ik):

T = {1 - ^{sin²
k' a}_{/4 E/V (1 −
E/V)}}^-1mit k' = (^2m(E-V)/_h²)^½

P.S. Für E = V erhält man nach l'Hopital (oder Potenzreihenentwicklung des Zählers und des Nenners):

T = {1 + ^ma²V/_2h²}^-1

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.