Wenn wir von zwei beliebigen Drehimpulsen 
1
und 2 ausgehen
(sei es der Bahndrehimpuls und Spin eines Elektrons oder der Bahndrehimpuls
zweier Elektronen), dann ist
J1² y
= j1(j1+1) h²
y
und J2²y
= j2(j2+1) h²
y
J1z y
= m1 h y
und J2zy
= m2 hy
 |
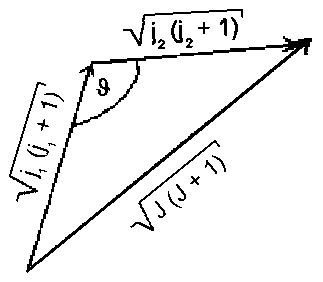| Abb.1.: Vektoraddition der beiden Drehimpuls j1 und j2 |
Für den Gesamtdrehimpuls
= 1 + 2 muss
gelten
J² y
= J(J+1) h² y
und Jzy
= m hy
m = −J, −J + 1, ... J
Welche Werte von J sind nun bei gegebenen J1 und J2 zulässig?
Nach dem nebenstehenden Vektormodell findet man relativ einfach, dass
der maximale Gesamtdrehimpuls Jmax durch
| Jmax = j1 + j2 |
und der minimale Gesamtdrehimpuls Jmin durch
| Jmin = |j1 − j2| |
gegeben ist, damit J ganzzahlige Werte annimmt.
 |
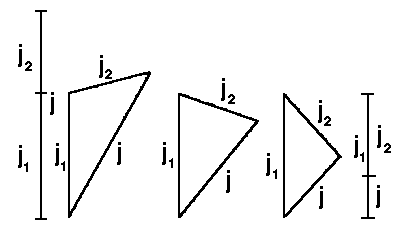| Abb.2: Zur Addition zweier Drehimpulse 1
und 2 zum
Gesamtdrehimpuls . Die Quantenzahlen
j1, j2 und j gehorchen der DreiecksUngleichung, wobei sich die erlaubten Werte von j um ganze Zahlen voneinander
unterscheiden. |
Die Quantenzahl für den Gesamtdrehimpuls J variiert also in Einerschritten von |j1 − j2| rauf bis j1 + j2 :
|j1−j2|, |j1−j2|+1, .......... , j1+j2−1, j1+j2
Der letzte Wert (j1 + j2) entspricht einer maximal
möglichen parallelen Ausrichtung zwischen 1
und 2; der
erste Wert einer quantenmechanisch maximal antiparallelen Ausrichtung.
Die Gesamtzahl der Zustände ist übrigens gleich:
Zu 1 gibt
es 2j1 + 1 mögliche Zustände (die m1).
Die Gesamtzahl ist dann (2j1+1)·(2j2+1),
denn zu jedem Zustand 1
gibt es (2j2+1) Zustände von 2.
Für jeden Gesamtdrehimpuls J gibt es 2J + 1 Zustände. Zur Abzählung haben wir also zu bilden:
J=|j1−j2| Σj1+j2 (2J + 1) = (2j1+1)·(2j2+1)
Wir können unser System also durch den Gesamtdrehimpuls
beschreiben, was natürlich sinnvoller ist, denn nur der Gesamtdrehimpuls
ist eine Erhaltungsgröße.
 |
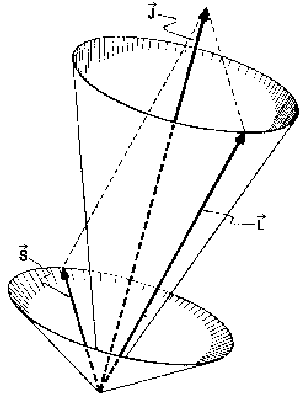Abb.3:  und 
bei der Spin-Bahn-Kopplung zum Gesamtdrehimpuls . Bezüglich einer vorgegebenen z-Richtung ist dieser richtungsquantisiert,
während und ,
die so um präzedierend
gedacht werden, dass die Dreiecks-Ungleichung erfüllt ist, unbestimmte
z-Komponenten haben. |
Einfachstes Beispiel für ein p-Elektron mir Spin s = ½ :
l = 1 , s = ½ (ml = −1, 0,
+1; ms = −½,
+½) ;
mögliche j-Werte laufen von |l-s|=½
in Einerschritten hoch bis l+s=3/2, also sind nur
j = ½ und j = 3/2
möglich.
| mj = { | −½, +½ für j = ½ |
| −3/2, −½, +½, +3/2 für j = 3/2 |
Hier werden kleine Buchstaben für die Quantenzahlen eingesetzt, da wir nur ein Elektron betrachtet haben; der allgemeine Fall - bei dem mehrere Elektronen zum Bahndrehimpuls bzw. Spin beitragen - kennzeichnen große Buchstaben die Quantenzahlen.
Die beiden Orientierungen des Spins ½ relativ zum Bahndrehimpuls l (>0) bewirkt eine Verdopplung der Energieniveaus, als Folge der so genannten Spin-Bahn-Wechselwirkung. Bevor wir uns dieser Wechselwirkung zuwenden, müssen wir noch den Einfluss eines Magnetfeldes auf "unser" Elektron behandeln.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.