Kohlenstoff:
z = 6
| n |
|
|
|||
| L | 2 |
|
Ý | Ý | |
| K | 1 | Ýß | C | ||
1s2 2s2 2p2
Der Gesamtspin kann 0 oder 1 sein. Der gesamte Bahndrehimpuls kann 0, 1 oder 2 sein, da jedes Elektron den Bahndrehimpuls 1 besitzt. |l1−l2| ≤ L ≤ ll + l2. Im folgenden wird eine Vorgehensweise erläutert, anhand der die möglichen elektronischen Konfigurationen für mehrere Elektronen mit einem Drehimpuls ungleich 0 ermittelt werden können. Im betrachteten Fall, dem Kohlenstoffatom, haben beide Elektronen die gleiche Quantenzahlen n und l, können sich also nur bezüglich (ml1, ms1) und (ml2,ms2) unterscheiden.
Tabelle 1 liefert den resultierenden Bahndrehimpuls ML und den resultierender Spin MS. Diese Werte gehen aus der Summation der einzelnen Bahndrehimpulse ml und Spins ms beider Elektronen hervor.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabelle 1: Ermittlung der möglichen Zahlenpaare (ML;MS) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Die erhaltenen Kombinationen (ML;MS) stellen Ausprägungen der Atomzustände 2S+1L J dar. Die Zuordnung zwischen dem Term 2S+1L J und den Zahlenpaaren beginnt beim höchsten Wert für L, hier ML = 2. Er ist einer Drehimpulsquantenzahl L = 2 beziehungsweise einem D-Term zuzuordnen. Diese Einstellung von ML tritt nur zusammen mit MS = 0 d.h. antiparallel ausgerichtetem Elektronenspins, auf. Konkret handelt es sich damit um einen 1D-Zustand. Ihm zugehörig sind ML Werte von -2 bis +2. Somit sind (2;0), (1;0), (0;0), (-1;0) und (-2;0) Ausprägungen des 1D Atomzustandes (vgl. Abbildung 1a). Als nächstkleinerer Wert von ML wird 1 angetroffen, beispielsweise im Zahlenpaar (ML;MS) = (1;1). Dieses Kombination rührt von einem Term mit L = 1 und S = 1, also 3P her, welcher das Zahlenpaar (1;1) und acht weitere Kombinationen einschliesst (vgl. Abbildung 1b). Die beiden bisher identifizierten Zustände repräsentieren 5 + 9 = 14 Kombinationen. Von den 15 aus Tabelle 1 hervorgegangen Kombinationen bleibt damit eine zurück, es handelt sich um (0;0). Sie ist die (einzige mögliche) Ausprägung eines Zustandes mit L = 0 und S = 0 (vgl. Abbildung 1c), das heisst, eines 1S0 Atomzustandes.
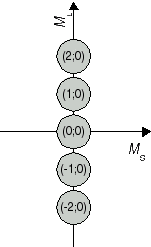 Abbildung 1a J=2 S=0 1D2 |
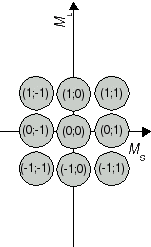 Abbildung 1b J=1 S=1 3P2,1,0 |
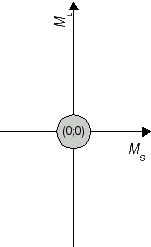 Abbildung 1c J=0 S=0 1S0 |
Wir erhalten demnach für die Zustände des Kohlenstoffatoms die drei Terme 1S0, 3P0, 3P1, 3P2 und 1D2. Die entsprechenden Termsymbole erscheinen in Tabelle 2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabelle 2: Die Zuordnung der Zahlenpaare zu Atomzuständen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Wegen der Hund'schen Regel (1) ist der Grundzustand ein Triplett-Zustand 3P. Die Hund'sche Regel (2) besagt, dass in unserem Fall einer weniger als halb gefüllten L-Schale der Zustand 3P0 energetisch tiefer liegt als 3P1 und 3P2. Er stellt damit den Grundzustand des Kohlenstoffatoms dar.
| C : K 2s2 2p2 ≡3P0 |
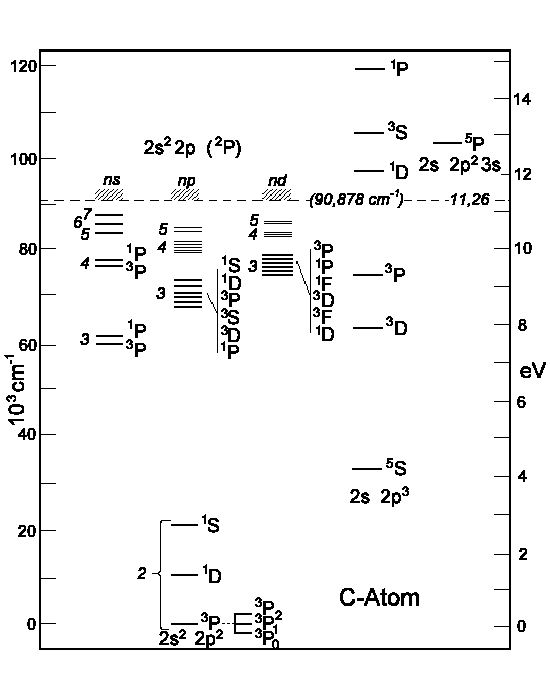
Die Energien zu den Termen 1S, 3P und 1D sowie die der angeregten Zustände des Kohlenstoffatoms sind Abbildung 2 zu entnehmen. Auf der rechten Seite sind die Energieniveaus angegeben, die sich bei Anregung eines 2s-Elektrons ergeben.
 |
|
| Abbildung 2: Energieniveaus beim Kohlenstoffatom. | |
| links: Anregung eines 2p-Elektrons. | rechts: Anregung eines 2s-Elektrons. |
Tabelle 3 zufolge gibt es für die p3 die Terme 4S, 2P, 2D. Hinzufügen eines 2s-Elektrons ergibt die Terme rechts.
So wie beim C-Atom im Grundzustand, der als Kombination zweier p-Elektronen dargestellt wurde, lassen sich auch die Zustände für andere Nebenquantenzahlen herleiten. Tabelle 3 listet die für verschiedene Belegungen möglichen und mit dem Pauli-Prinzip vereinbaren Terme von Atomen mit Elektronen in s-, p- und d-Orbitalen auf.
| Konfiguration | Term | Konfiguration | Term | |
|---|---|---|---|---|
| s
s2 p, p5 p2, p4 p3 |
2S
1S 2P 1S, 1D, 3P 4S, 2P, 2D |
d, d9
d2, d8 d3, d7 d4, d6 d5 |
2D
1S, 1D, 1G, 3P, 3F 2D, 2F, 2G, 2H, 4P, 4F 1S, 1D, 1F,1G,1I,3P,3D,3F,3G,3H,5D 2S, 2P, 2D,2F,2G,2H,2I,4P,4D,4F,4G,6S |
|
| Tabelle 3: Atomzustände für verschiedene Belegungen von s, p und d-Atomorbitalen | ||||
Stickstoff:
z = 7
| n | s |
|
|||
| L | 2 |
|
Ý | Ý | Ý |
| K | 1 | Ýß | N | ||
(1s2) ( 2s2) ( 2p3)
Nach Hund'scher Regel sollen die Spins möglichst parallel ausgerichtet
sein, so dass der Gesamtspin S = 3/2
wird. Nach der Tabelle oben kommen die drei Terme 4S, 2P,
2D
für die Kombination der drei p-Elektronen in Frage. Also ist der Gesamtzustand:
| 4S3/2 |
Sauerstoff:
z = 8
| n |
|
|
|||
| L | 2 |
|
Ýß | Ý | Ý |
| K | 1 | Ýß | O | ||
(1s2) ( 2s2) ( 2p4)
Nur scheinbar wird es bei 4 p-Elektronen komplizierter; denn eine andere Betrachtungsweise erlaubt eine deutliche Vereinfachung der Kombination von 4 p-Elektronen:
Wir wissen, dass mit 6 p-Elektronen (p6) die Schale
gefüllt ist, also L = 0 und S = 0 ist. Wir können uns das Sauerstoffatom
nun so vorstellen, als ob 2 Elektronen einer (p6)-Schale fehlen
würden. Diese fehlenden Elektronen oder Defektelektronen oder auch
Löcher werden nun nach den möglichen "Zweiloch-Konfigurationen"
arrangiert, denn die Löcher haben ebenfalls den Spin ½. Somit
haben wir beim Sauerstoff wie beim Kohlenstoff die möglichen Zustände
1S,
3P,
1D.
Der höchste Spin (Hundsche Regel (1))
ist S = 1, d.h. der 3P ist Grundzustand und der Gesamtdrehimpuls
J ist für den Grundzustand (Hundsche Regel (2))
J = L + S = 2. Also:
| 3P2 |
Fluor:
z = 9
| n |
|
|
|||
| L | 2 |
|
Ýß | Ýß | Ý |
| K | 1 | Ýß | F | ||
(1s2) ( 2s2) (2p5) : 2P3/2
Es fehlt ein p-Elektron, d.h. L = 1 und S = ½.
J = ½ und 3/2 sind
möglich. Nach Hundscher Regel (2) ist
der größere J-Wert für den Grundzustand gültig:
| 2P3/2 |
| n |
|
|
|||
| L | 2 |
|
Ýß | Ýß | Ýß |
| K | 1 | Ýß | Ne | ||
(1s2) (2s2) (2p6) : 1S0
2p-Schale ist voll ! Hohe Ionisierungsenergie von 21,6 eV
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.