Wavepacket:
a hybrid between a wave and a particle
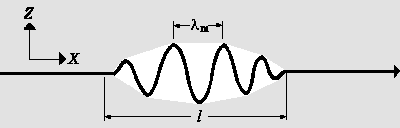The wavepacket and its Fourier components
a) Wavepackets are boundless sine-like waves which layer on top of each other. This is shown below
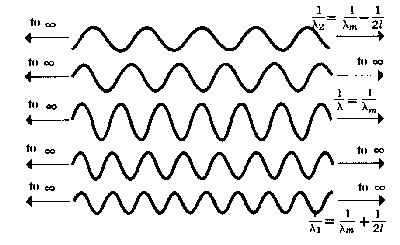b) Few Fourier components of wavepacket

One can obtain particles from waves by constructig a wavepacket. A wavepacket is a wave which is limited to the spatial region shown in the Figure. Since the probability of finding the particle at any given point is proportional to the amplitude squared, there is a high probability of finding the particle somewhere inside the area delineated by the wave packet. Conversely, the probability of finding the particle outside this area  is almost 0. Therefore the possible value for x-coordinate of the particle spreads over the small region of length l:

Δx  =  l

If we use the length l as the wavelength of the wavepacket and we use the following definition of momentum we have: 

pm  =  h/λm

However, the strict mathematical formulation of quantum mechanics only lets us apply this relationship to boundless sine-like waves. Fortunately, a wavepacket of finite length can be represented by a boundless sine-like wave These sine-like waves with differing wavelengths are referred to as theFourier components of wavepacket (Joseph Fourier). When the wavelengths (or frequencies), amplitudes and phases of these waves are chosen in such a way that they coincide with each other in time it produces the wave illustrated in the uppermost figure of this page. 

Almost all Fourier components have wavelengths that lie between λ1 and λ2, having the following meanings

1/λ1  = 1/λm + 1/2l     oder     1/λ2  =  1/λm− 1/2l

The meaning of λm lays between λ1 and λ2. The corresponding impulses are the following:

p1  =  h/λ1  =  h/λm + h/2l  =  pm + h/2l

and

p2  =  h/λ2  =  h/λm− h/2l  =  pm − h/2l

That's why the impulse corresponding to the wavepacket isn't a precisely defined quantity.Rather it is spread out in the following region: 

Δpx  ≈  p1 − p2

or
Δpx  ≈ h/l

From this formula and Δx = l one can obtain
 

Δpx Δx ≈  h

The Heisenberg uncertainty principle is the key concept that describes the behavior of such wavepackets.  

In the case of the electron (or any other particle with the nonzero rest mass) each Fourier component is the de Broglie wave. The de Broglie wave speed is as follows

V  =  cē/v

The expression for particle momentum, p = h/λ, and p = mv is the mathematical meaning of Fourier component wavelength λ which has a definite speed  symbolized by V. The speed V of different Fourier components differs for different wavelengths. This is similar to dispersion phenomenon where light passes through glass.  Due to the large amount of Fourier components in one wavepacket, the fourier components are dispersive.  The wavepacket pictured at the top of the screen is not static in time. 
The next process (time dependence) is shown in the following illustration.
 
The divergence of the de Broglie wavepacket when spreading in the space.
If the wavepacket moves forward, it spreads out in space. The speed of the left border point L is slower than the speed of right border point R.  This is caused by the uncertainty principle (because the particle speed isn't exactly defined). The envelope line of wavepackets will be clear when one looks at the illustration with the border between the light wavepackets and the dark background. P is the envelope line maximum point. The speed of point P is also referred to as the group speed of the wavepacket 
 

vm  =  pm/m  =  h/mλm

The speed of P is the average speed of a particle, which is a reasonable result. 

Now we can disprove that de Broglie's wave speed cē/v is not equal to v and larger than c. Look at the wave inside the envelope line and the wave crest p which is marked by bold point on the illustration. This wave crest p moves faster than the envelope line maximum P

Vm  =  cē/vm

This is the Fourier component speed which has the average wavelength λm. And is referred to as the wavepacket phase speed. That's why the wave crest p moves faster than the envelope line from left end L towards right end R of the wavepacket. The waves always come from L and disappear at R. 

We should not be concerned if the phase speed Vm is greater than the speed of light c.  The importantant electron structure stays inside of the envelope line (which has the group speed  vm) and slowly moves forward while never quite reaching the speed of light.  
One can find some Java-Applets which describe the movement of wavepacket here. 


Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.