Complex Numbers and Functions

The real number domain can be broadened up to the complex numbers, for
instance the square root of negative real number is not defined in the real
number domain. The complex number c can be represented as the vector of ordered
pair (a,b) having a corresponds to pure real number (a,0) and b corresponds to
pure imaginary number (0,b). The complex numbers are often represented in a
following way
c = Re c + iIm c = a + ib
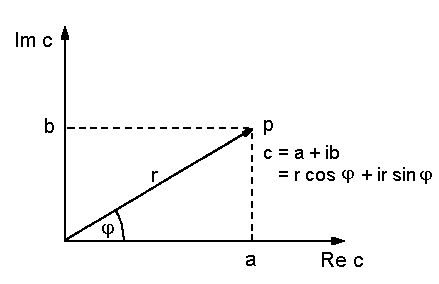 |
| Fig. 1: Complex numbers |
One can see from Figure 1 that whether you know r (=point P vector) and angle j
it's possible to unambiguously determine c (complex number value). The Euler
Formula:
c = a + ib = r (cos j
+ i sin j) = r ·
eij
where r² = a² + b² and tan j =
b/a.
Important complex number rules:
-
a.
Addition (subtraction is analogous having minus sign)
c1 + c2 = (a1 + a2,
b1 + b2) = (a1 + a2)
+ i(b1 + b2)
-
b. Multiplication
c1 · c2 = r1eij1
− r2eij2
= (r1 · r2) ei(j1
+ j2)
-
c.
Division
c1/c2
= r1/r2
ei(j1 −
j2)
-
Exponentiation
cn = rn eijn
-
Complex-conjugate number c*
c* = a − ib = re−ij
-
Absolute value
Ö(|c|²)
= Ö(cc*)
= Ö(reij
re−ij)
= r
-
Polar representation
i = eiπ/2
with i² = −1
The complex numbers representation is applied for instance when describing phase
shifts alterations between alternate currents and voltages (complex resistance =
impedance) or between electric alternate field and induced polarization (complex
dielectric constant). The complex numbers are also used in description of
periodical processes with e-functions serving Euler formula for real and
imaginary amplitudes recalculation.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
