The Schroedinger Equation

The fundamental equations of quantum mechanics lead us to the Schroedinger equation printed below. One must produce equations which comply with the schrodinger equation and experiemental measurements. You can find one of the derivations of Schroedinger equation here.

We can write down the following differential equation for probability amplitude when the process doesn't depend on time:
 

time independent Schroedinger equation:

[− h²/2m∂²/∂x² + V(x)]y  =  E y

where V(x) is the potential that acts upon particle t. If we substitute p2/2m (that is directly corresponds to the kinetic energy) for (−h²/2m∂²/∂x²) we follow the law of energy conservation. If we substitute E for  ih∂/∂t then it'll be the following
 

time dependent Schroedinger equation:

[− h²/2m∂²/∂x² + V]y  =  ih ∂/∂ty

We can also obtain the three dimensional (x,y,z) equation, if we substitute ∂²/∂x² for ∂²/∂x²+∂²/∂y²+∂²/∂z². Erwin Schroedinger was the first scientist who solved this equation for hydrogen atom (as a three dimensional problem). All experimental verifications show that Schroedinger equation fully holds true in non-relativistic quantum mechanics. Since all chemical processes run with a speed slower than speed of light then one can say that the Schroedinger equation is a torch of truth for chemists which gives light to a dark road of interactions between atoms and molecules.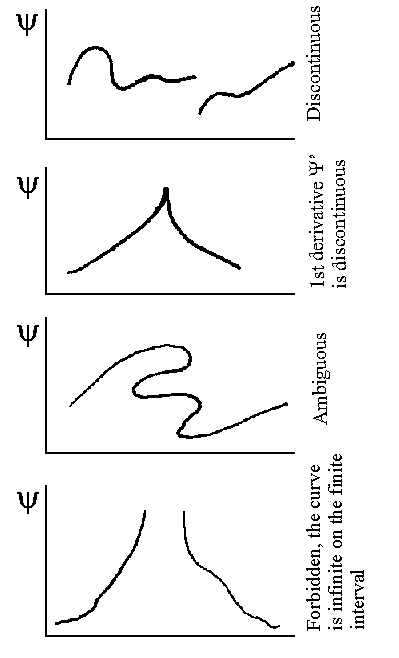
The wavefunction y as it has been mentioned earlier has no direct physical sense. Since the probability of detecting a particle somewhere in a space is equal to 1, we can write the normalization condition:
 

 -¥ò+¥|y(x,y,z)|2dx dy dz = 1 

The expression |y(x,y,z)|2dxdydz shows the probability P(x,y,z) of detecting a particle in a position with coordinates (x,y,z) in a volume unit dV = dxdydz. P(x,y,z) unlike y(x,y,z) has direct physical meaning because the probability can be measured in experiments.

Wavefunction y requirements:

  1. The second derivative of a function which is acted upon by the schrodinger equation should have a second derivative that is continuous. The first derivative should also be continuous and give "reasonable" meanings. (for instance, the 1/r-potential when r=0)
  2. Finally, according to simple physical principles, one can suppose y to be unambiguous and never unlimited (|y|2dxdydz) < ¥).
The probability amplitude y describes considered system completely and we can obtain all necessary information about our system using it. 
 
 

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.