(A Particle in Potential Well)
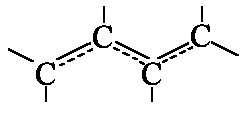 |
In bounded systems like
![]() etc. the π-electrons can move along the whole chain
length. They "behave" like one-dimensional "electron gas". Let's study the
electron movement and moreover idealize our polyene a bit further.
etc. the π-electrons can move along the whole chain
length. They "behave" like one-dimensional "electron gas". Let's study the
electron movement and moreover idealize our polyene a bit further.
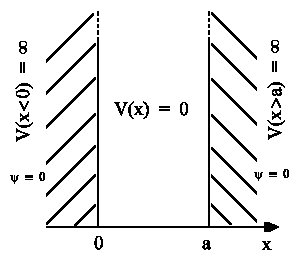 |
This simple model for polyene description strictly corresponds to
particle movement in potential well
having potential value V(x)=0 in the range
0 < x < a . Solving
the corresponding Schroedinger equation:
| d²y/dx²
+ 2mE/ |
one obtain rational physical solutions only when energy possesses definite
(rather than continuous) discrete values:
| En = h²/8ma² n² where n = 1, 2, 3, ... |
The energy should be quantized since n is integer. The possible energy values are then: E1 = h²/8ma² , E2 = 4E1 , E3 = 9E1 , E4 = 16E1 ,.... This energy quantization happens because of wavefunction is restricted to boundary conditions and potential.
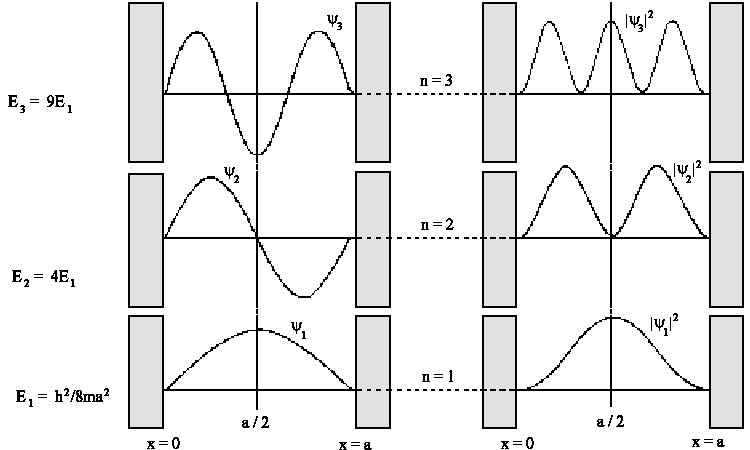
| yn(x) = (2/a)½ sin(nπx/a) |
Using the above figure one can see that only the stationary wavefunctions are possible. The lowest energy state n=1 has only one maximum and only two minimum on its sides. Having new higher energy state we will also have one more wavefunction zero. One also can see that the wavefunction holds symmetry in its middle: its value is either the same or it changes its sign upon wavefunction reflection. It's said about positive parity when the wavefunction sign is the same [y(a/2+x) = +y(a/2-x)] upon wavefunction reflection relative to symmetry axis that is x=a/2 and about negative parity whether the wavefunction sign is changed upon reflection [y(a/2+x) = -y(a/2-x)], correspondingly.
All free (and certainly possible) quantum states are fulfilled with electrons
having corresponding energies. According to Pauli exclusion principle we will
obtain having in mind spin definition (since electrons are Fermi particles):
| Butadiene |
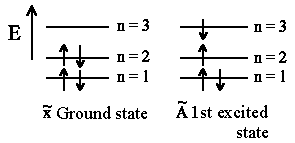 |
One can observe absorption spectra of polyenen and excitation energy ΔE that corresponds to energy difference between two successive states with (n+1) and n. We will assign the highest energy level in the ground state that is occupied by electrons as HOMO (highest occupied molecular orbital). For butadien it's n = 2. The energy level that lays upper than HOMO (it is n+1=3 for butadien) is also referred to as LUMO (lowest unoccupied molecular orbital). According to Pauli exclusion principle we can put at most 2 electrons having opposite directed spins (spin up and spin down) on one level. Hence total number of double bindings corresponds directly to n and finally we obtain ΔE = En+1 − En as energy difference between successive levels:
ΔE = h²/8ma²[(n + 1)² − n²] = h²/8ma² (2n + 1) = hν = hc/λ
where λ is the absorption wavelength. And if we measure the absorption wavelength, it's also possible to obtain experimental chain length a from it:
aexp2 = (2n+1) λexp. h/8mc
The C-C binding length is about ao≈
0,139 nm so one can write down akk
= ao.
(2n−1) for the length of one section.
Experiment has given us the following results:
| n | Stoff | lexp / nm | ® aexp / nm | akk / nm |
| 2 | Butadien | 210 | 0,56 | 0,42 |
| 3 | Hexatrien | 247 | 0,72 | 0,70 |
| 4 | Octatetraen | 268 | 0,88 | 0,98 |
| 5 | Vitamin A | 306 | 1,01 | 1,26 |
| 11 | Carotin | 420 | 1,70 | 2,94 |
Although the model was extremely simple it gives reliable results.
And now let's consider electricity conductive polymers:
The Nobel Prize of 2000 was given to A.G. MacDiarmid, A.J. Heeger and H. Shirakawa
for their proceedings in the chemistry of conductive polymers. The conductivity
of metals is based on that the upper free states can be occupied by any external
electrons with high energy which they can obtain in thermal way: the occupied
and upper free states are situated very close to each other in metals. Contrary
to metals there are isolators: they have great gap between HOMO and LUMO
orbitals. Conjugated polymers are situated between metals and isolators that
means their gap between HOMO and LUMO decreases when increasing chain length.
If we substitute into our equation for energy gap between LUMO and HOMO ΔE = h²/8ma² (2n+1) for a section length a = ao·(2n−1) of a chain:
ΔE = h²/8mao² · (2n+1)/(2n-1)²
For high n values ΔE = h²/6mao² · 1/n , i.e. ΔE is becoming smaller when increasing chain length and that's why the conductivity is increasing since external electrons can move to higher unoccupied states in more easy way.
Nevertheless more precise quantitative chemistry shows that the gap is decreasing but there is pure polyacetylen which has conductivity only about 10−7 - 10−5 siemens per meter that is like usual semiconductor material. The reason is that each second binding is double binding.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.