Translational Degeneracy

The energy levels of a particle in 3-dimensional box are as follows

E  =  h²/8ma²(n1² + n2² + n3²)  =  h²/8ma²· K² =  E1 · K²

All combinations n1, n2 and n3 that give finally the same K value have the same energy and therefore it's said these energy levels are degenerate. This degeneracy degree, which is assigned by quantity g, corresponds to number of independent wavefunctions.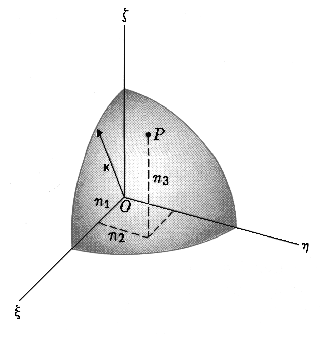 

The number of energy levels within a small energy region dE can be calculated now for a particle situated in a big potential well. The states amount N(E) beginning from zero energy and till energy E corresponds to sphere volume that has radius K (K² = n1²+n2²+n3²) divided by 8 since only positive values of n1, n2 and n3 are resolved:

N(E)  =  1/8(4/3πK3)  =  π/6 V (8mE/h²)3/2

The second equality sign is obtained from E = h²/8ma²·K² and K= a·(8mE/h²)1/2  and V = a³. Differentiating the last formula by dE, one can obtain the number of states in the range [E, E+dE]:

d N(E)  =  [4πV(2m³)½/h³] E½ dE


 

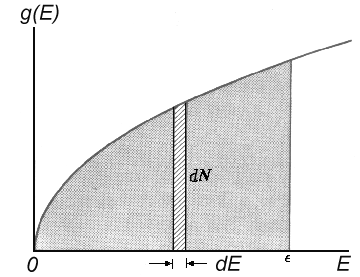The energy levels density g(E) = dN/dE, i.e. the number of states per energy unit range is then as follows:
 

g(E)  =  4πV(2m³)½/h³. E½

Here we've just obtained the statistical sum:

Q  =  oò¥ e−E/kT g(E) dE
Q  = 4πV/h³ (2m³)½ oò¥ E½ e−E/kT dE
ß
Q  =  V/h³ (2πmkT)3/2

Moreover, we've obtained a very important quantity: the number of state translations. One can get all thermodynamical quantities (relatively translation) from the calculations considered. 


Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.