Der Tunneleffekt (Herleitung)

The Tunneling Phenomenon - Treatment

Let's consider a particle with mass m which is moving with energy E (from left side) up to potential barrier having width a:

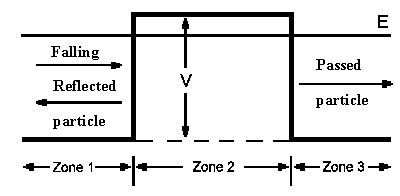
Zone 1

Zone 2

Zone 3

^h²/_2m^d²/_dx²y₁ + Ey₁ = 0

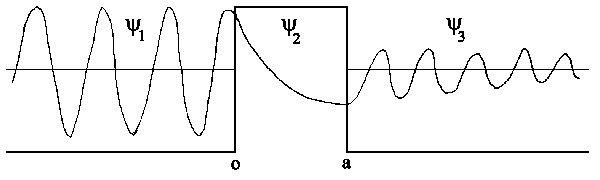
y₁ = A₁e^ik1^x + B₁e^−ik1^x

k₁² = 2m ^E/_h²

^h²/_2m^d²/_dx²y₂+(E -V)y₂ = 0

y₂ = A₂ e^ik2^x + B₂ e^−ik2^x

k₂² = 2m ^(E−V)/_h²

^h²/_2m^d²/_dx²y₃ + Ey₃ = 0

y₃ = A₃ e^ik3^x + B₃ e^−ik3^x

k₃² = k₁² = 2m ^E/_h²

If the particle energy E is smaller than V in zone 2: k₂²< 0, i.e. k₂ is imaginary number. If we write down k₂ = ik where k is real number now k²= 2m ^(V−E)/_h² then we will obtain the following wavefunction in zone 2:

y₂ = A₂ e^−k^x + B₂ e^kx

This function doesn't vibrate but shows the exponential dependence on x.

Now we will calculate coefficients A_i and B_i (i = 1, 2, 3). Since particles come from the left side the coefficient B₃ should be 0 because the wavefunction B₃ e⁻ⁱ^k1^x corresponds to particles moving from right to the left. However there are no such particles ! The coefficient B₁ should not be 0 since particles can be reflected by potential barrier and then move back to the left. Another coefficients can be obtained from boundary conditions and normalization: y and y' should be continuous

	x = 0	x = a
y continuous:	A₁ + B₁ = A₂ + B₂	A₂ e^−k^a + B₂ e^k^a = A₃ e^ik1^a
y' continuous:	ik₁A₁ − ik₁B₁ = −kA₂ + kB₂	-kA₂ e^−k^a + kB₂ e^ka = ik₁A₃ e^ik1^a

The coefficient B₁ determines the probability (|B₁|²) for the particle to be reflected and the coefficient A₃ corresponds to the probability (|A₃|²) for the particle to pass through potential barrier V and then move along the right side with hk. The transmission probability T = |A₃|²/|A₁|² corresponds to the chance for particle to cross a barrier. Simple but detailed transformations of the above-mentioned boundary conditions give finally:

T = {1 + [e^k^a− e^−k^a]²_/[16 ^E/_V (1-^E/_V)]}^-1 where k = (^2m(V-E)/_h²)^½

or T = {1 + sinh²(ka)_/[4 ^E/_V (1-^E/_V)]}^-1

Although E < V the transmission probability T isn't equal to 0, i.e. a particle can cross the potential barrier that isn't allowed in classical physics.
The wavefunction isn't equal to 0 at point x=0 since V is finite in height and width. One can write down the following approximation for ka > 1:

T ≈ 16 ^E/_V(1 − ^E/_V) e^−2ka

For E > V T can be < 1 , which means that particles are reflected back even if the particle energy is greater than the barrier height. Here one can write down (k' = ik):

T = [1 - ^{sin²
k' a}_{/4 E/V (1 −
E/V)}]^-1where k' = (^2m(E-V)/_h²)^½

P.S. One can also write down for E = V (after Taylor expansion of numerator and denominator):

T = [1 −^ma²V/_2h²]^-1

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.