If we have any two angular momentums 
1 und 2
(it's an orbital angular momentum and electron spin or orbital angular momentum of two electrons)
we will have:
J1² y = j1(j1+1)
h² y
and J2²y
= j2(j2+1) h² y
J1z y = m1 h y
and J2zy
= m2 hy
 |
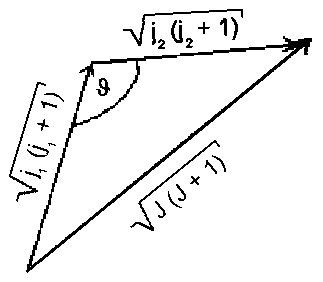| Fig.1.: Vector addition of two angular moments j1 and j2 |
For total angular momentum = 1 + 2
it should be the following
J² y
= J(J+1) h² y
and Jzy
= m hy
m = −J, −J + 1, ... J
What values of J are possible for given J1 and J2?
After introducing simple vector model the total maximum angular momentum will
be as follows
| Jmax = j1 + j2 |
and the total minimum angular momentum Jmin :
| Jmin = |j1 − j2| |
where J takes on only integer values.
 |
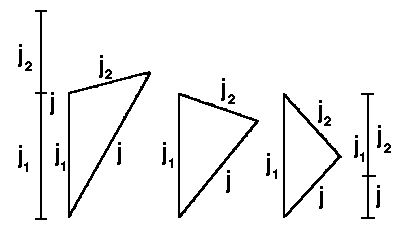| Fig.2: The addition of two angular moments
1
and 2 into the total angular momentum . The quantum numbers
j1, j2 and j obey to the vector addition rule.
|
The quantum number of angular momentum can take all possible values in the range from |j1 − j2| to j1 + j2 :
|j1−j2|, |j1−j2|+1, .......... , j1+j2−1, j1+j2
The last possible value (j1 + j2) corresponds to
maximum possible parallel alignment between 1 and 2; and the
first value corresponds to maximum antiparallel alignment. The total number of
alignments is as follows:
For 1 there are
2j1 + 1 possible states (m1). And so the total possible
amount of states is (2j1+1)·(2j2+1) since there are
(2j2+1) states of 2 for each 1 state.
For any angular momentum J there are 2J + 1 states:
J=|j1−j2| Σj1+j2 (2J + 1) = (2j1+1)·(2j2+1)
We can describe our system by using total angular momentum , which is more definitely more rational because only the total angular momentum stays the same.
 |
Fig.3:  and  in the spin-orbital
interaction with the total angular momentum . |
The simplest example for p-electron having spin s = ½ :
l = 1 , s = ½
(ml = −1, 0, +1; ms =
−½, +½) ; the possible j-values begin from |l-s|=½ and end by l+s=3/2 and that's why
the only possible values are j = ½ and j =
3/2.
| mj = { | −½, +½ for j = ½ |
| −3/2, −½, +½, +3/2 for j = 3/2 |
Here we assign the quantum numbers by small letters as we have already seen in the example with electrons; the general case when one has a lot of electrons creating orbital angular momentum and spin are characterized by big letters which correspond to quantum numbers.
The levels doubling as a consequence of above-mentioned interaction between spin and orbital angular momentum gives rise to orientation of spin ½ relative to orbital angular momentum l (>0). Before we will come to this interaction we first must have a look at influence of magnetic field on our electron.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.