The results listed below go to the eigenfunctions and eigenvalues of the
squared kinetic moment and z-component of the kinetic moment. One can find the
detailed derivation demanding knowledge of the commutativity relations
here.
One can obtain for the eigenvalues:
| L² Yl,m
= l (l +1) Lz Yl,m
= m |
| − l ≤ m ≤ l |
The calculation here shows m can only be integer. Since the smallest m value (m = - l) corresponds to the sum of the highest possible m value (m = l) l can be either half-integer or integer. Given l there are 2l + 1 values of m. The half-integer values correspond to spin. The corresponding eigenfunctions are not the space coordinates functions and they can't be derived from the Schroedinger equation. The half-integer eigenvalues of the knetic moment can only be obtained by the kinetic moment operator conversion. Firstly we would like to have a look at the integer eigenvalues, i.e. l can be 0,1,2,3,... and m begins from m = -l and lasts till m = +l.
|
L² Yl,m
= l (l +1) Lz Yl,m
= m |
The eigenfunctions of the kinetic moment z-component depend only
on angle j therefore we can choose the following
separation of variables:
| Yl,m(J,j) = | P(J) | · | φ(j) |
| f(j) = (2π)-½ eimj |
The functions of angle J for
m = 0 is called the Legendre
Polynomial (Pl(cosJ))
and for m ¹ 0 it is also called the
associated
Legendre Polynomial (Pl,m(cosJ);
it's sometimes written by using superscript index m: Plm(cosJ)).
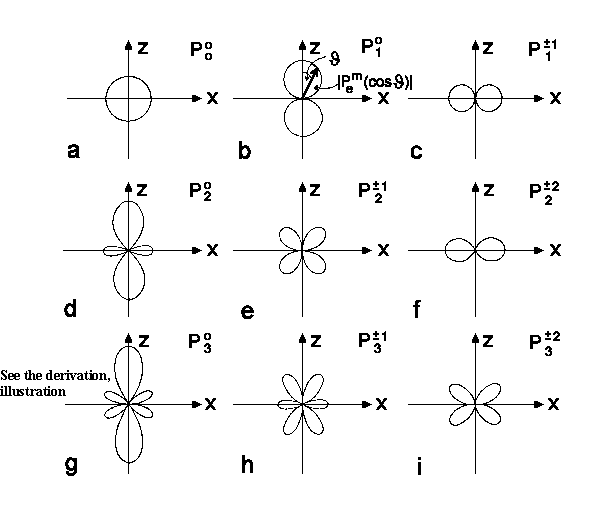
All the Legendre Polynomials Plm(cosJ)
till l =3 are represented in the polar coordinates on the next figure.
Moreover we obtain the function absolute sum which depends on the angle as the
radius vector of this angle relative to the z-axis. For your recalling:
and the same in polar coordinates:
 |
|
| Fig.1a-k:
The polar coordinate J-dependence
illustration
Legendre Polynomial (a,d,g) and associated Legendre Polynomial. |
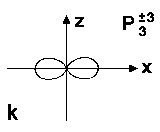 |
see Fig.1g-k for P3m |
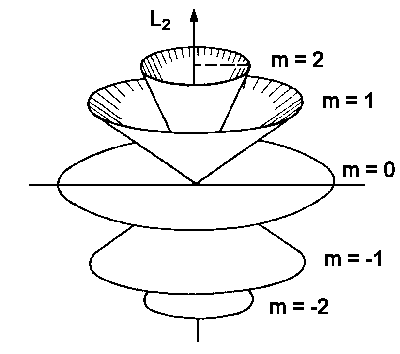
| Fig.2: The space quantization: a number of possible kinetic moment L alignments having the kinetic moment quantum number l = 2. |
The total function Yl,m(J,j)
= P(J)·f(j)
is called the Ball area
function.
The normalization of ball area function originates from the integration over
corresponding volume ("angle") dW
= sinJ dJ
dj:
| o∫2π | oòp | |Yl,m|² | sinJ dJ dj | = 1 |
| j | J | |¾¾¯¾¾| | ||
| dΩ | ||||
The normalized ball area
functions for l
= 0, 1, 2, 3, 4
|
Yl,m(J,j)
= Plm(cosJ)
·φm
(j)
φm (j)
= 1/(2π)½ eimj
|
||||
| Electron | l | m | Yl,m(J,j) | Yl,m Yl,m* |
| s | 0 | 0 | 1/(4π)½ | 1/4p |
| p | 1
1 |
±1
0 |
±(3/8p)½
sinJ e±ij
(3/4p)½ cosJ |
3/8p
sin²J
3/4p cos²J |
| d | 2
2 2 |
±2
±1 0 |
(15/32p)½
sin²J e±2ij
±(15/8p)½ sinJcosJ e±ij (5/16p)½ (3cos²J − 1) |
15/32p
sin4J
15/8p sin²Jcos²J 5/16p (3cos²J- 1)² |
| f | 3
3 3 3 |
±3
±2 ±1 0 |
(35/64p)½
sin3J e±3ij
(105/32p)½ sin²JcosJ e±2ij (21/64p)½ sinJ (5 cos²J - 1) e±ij (7/16p)½ (5 cos3J − 3 cosJ) |
35/64p
sin6J
105/32p sin4Jcos²J 21/64p sin²J (5 cos²J- 1)² 7/16π (5 cos3J − 3 cosJ) |
| g | 4
4 4 4 4 |
±4
±3 ±2 ±1 0 |
(315/512p)½
sin4J e±i4j
(315/64p)½ sin3JcosJ e±3ij (225/660p)½ sin²J (7 cos²J- 1) e±2ij (225/320p)½ sinJ (7 cos3J- 3 cosJ) e±ij (9/256p)½ (35 cos4J − 30 cos²J + 3) |
315/512p
sin8J
315/64p sin6Jcos²J 225/660p sin4J (7 cos3J- 1)² 225/320p sin²J (7 cos3J- 3 cosJ)² 9/256π (35 cos4J − 30 cos²J + 3)² |
The ball area function equations are very hard to plot because of the imaginary j-dependence in the exponent:
φm(j) = 1/(2π)½ eimj m = 0, ±1, ...
Therefore we will use special linear combinations of functions:
χ+ º f(+m)
= e+i|m|j = cos mj
+ i sin mj
c- º f(−m) = e−i|m|j = cos mj -
i sin mj
It's very interesting! Why can we do it in so arbitrary way? We can do it in this way because of the following
| Any linear combination of confluent eigenfunctions is the eigenfunction
again of corresponding operator:
φ = c1 χ1 + c2 χ2 → Linear combination F χ1 = Fe χ1 and Fχ2 = Fe χ2 Confluent, i.e. similar eigenvalue Fe for both functions χ1 and χ2 F φ = c1 F χ1 + c2 F χ2 = Fe (c1 χ1 + c2 χ2) = Fe φ
|
Now we take the two linear combinations:
φ+ ~ 1/2 (χ+ + c-) = cos mj
f- ~ 1/2i (χ+ -c-) = sin mj
and obtain real functions after normalization
| φ+ =
1/p½
cos
mj
f- = 1/p½ sin mj |
So we can produce real functions which are utterly useful for chemical
analysis. One can find functions for l and |ml| in the next
table:
| l | ml | ball area function |
| 0 | 0 | s = 1/(4π)½ |
| 1 | 0 | pz = (3/4π)½cosJ |
| +1 | px = (3/4π)½sinJcosj | |
| -1 | py = (3/4π)½sinJsinj | |
| 2 | 0 | d3z²−r² = (5/16π)½(3 cos²J - 1) |
| +1 | dxz = (15/4π)½sinJcosJcosj | |
| -1 | dyz = (15/4π)½sinJcosJsinj | |
| +2 | dx²−y² = (15/16π)½sin²Jcos2j | |
| -2 | dxy = (15/16π)½sin²Jsin2j |
States having different l are characterized by the following letters (according to historical reasons):
l = 0,1,2,3,4,5,6,7,8,...
s,p,d,f,g,h,i,k,l,...
The lowest s-state (l = 0) is isotropic; if there is spherical symmetry. It means on the polar diagram that we obtain the spherical shell since the s-function meaning is equal in all directions (J, j). It's clear because there is no selected orientation for zero electron motion.
For l = 1, or p-state, there are three trigonometric functions px, py, pz that describe possible electron movement along 3 coordinate axes and therefore they are important for chemical bounding description.
For l = 2, or d-state, there are 5 trigonometric functions which are a bit complicated to be plotted. For higher l values (g, h, j...) such figure would be much harder to plot.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.