From Carbon to Neon

From Carbon To Neon

Carbon:
z = 6

n s p

L 2 Ýß Ý Ý

K 1 Ýß C

1s² 2s² 2p²

The total spin can be 0 or 1. The total orbital momentum can be 0, 1 or 2 since either electron possesses an orbital momentum of 1. |l₁−l₂| ≤ L ≤ l₁ + l₂. Now let's try to explain possible configurations with l ≠ 0. Primarily, both p-electrons have common quantum numbers n and l; therefore only the quantum numbers (m_l1, m_s1) and (m_l2, m_s2) remain to be considered. m_l1 and m_l2 may be equal to -1, 0, +1 and m_s1 and m_s2 may be equal to -½, +½.

Table 1 contains the results for the total orbit momentum M_L and the total spin M_S. These values represent the sum of the orbit momenta m_l and of the spins m_s of the two electrons.

Six combinations are excluded due to Pauli's principle which forbids that one pair of electrons is described by identical sets of quantum numbers. "X" appears in the respective cells.
As we have only one kind of electrons and our labelling "1" and "2" is fictional, there are only 15 instead of 30 possible combinations. The cell's content "s.a." (for "see above") indicates that the combination is described in a cells above the table's diagonal.

e^-	1.
2.	m_l		-1		0		+1
		m_s	-½	½	-½	½	-½	½
	-1	-½	X	( -2; 0)	(-1;-1)	(-1; 0)	( 0;-1)	( 0; 0)
	-1	½	s.a.	X	(-1; 0)	(-1; 1)	( 0; 0)	( 0; 1)
	0	-½	s.a.	s.a.	X	( 0; 0)	( 1;-1)	( 1; 0)
	0	½	s.a.	s.a.	s.a.	X	( 1; 0)	( 1; 1)
	+1	-½	s.a.	s.a.	s.a.	s.a.	X	( 2; 0)
	+1	½	s.a.	s.a.	s.a.	s.a.	s.a.	X

Table 1: Determination of resultant pairs of M_L and M_S

The recieved combinations (M_L;M_S) belong to atomic states ^2S+1L _J. In a second step, we determine the respective states. We start with the highest value for L, i.e. M_L = 2. From this M_L, we conclude that the two electrons produce an atomic state with L = 2 which is denoted with a capital D in the term symbol. Both extremes, M_L = 2 and M_L = -2 are combined with M_S = 0, i.e. an antiparallel orientation of the two electron spins. Therefore, we have state ¹D. The calculated pairs (2;0), (1;0), (0;0), (-1;0) and (-2;0) are special cases for the carbon atom in state ¹D (compare Fig. 1a). As next value, M_L = 1 has been obtained, for example in (M_L;M_S) = (1;1). This combination is one out of nine cases which emerge from assuming an atomic state with L = 1 and S = 1. The respective state is denoted as ³P state. (compare Figure 1b). So far, 5 + 9 = 14 of our set of 15 have been identified as cases of two states. The remaining pair (0;0) is the only case for a state with L = 0 and S = 0 (compare Fig 1c); in other words, an atomic state ¹S₀.

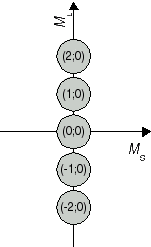Fig. 1a
J=2 S=0 ¹D₂

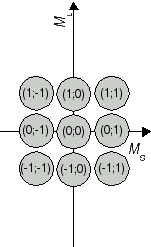Fig. 1b
J=1 S=1 ³P_2,1,0

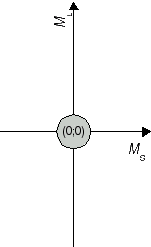Fig. 1c
J=0 S=0 ¹S₀

Therefore, dependent on the distribution of electrons and their spins, the carbon atom exists in states denoted by the term symbols ¹S₀, ³P₀, ³P₁, ³P₂ and ¹D₂. These symbole have been introduced in table 2.

e^-	1.
2.	m_l		-1		0		+1
		m_s	-½	½	-½	½	-½	½
	-1	-½	X	¹D	³P	³P	³P	¹S
	-1	½	s.a.	X	¹D	³P	³P	³P
	0	-½	s.a.	s.a.	X	¹D	³P	³P
	0	½	s.a.	s.a.	s.a.	X	¹D	³P
	+1	-½	s.a.	s.a.	s.a.	s.a.	X	¹D
	+1	½	s.a.	s.a.	s.a.	s.a.	s.a.	X

Table 2: The combinations are representations of three atomic states

According to Hund's rule (1) the ground state is ³P and according to rule (2) is the ³P₀ state.

C : K 2s² 2p² ≡³P₀

Other energy terms than ¹S, ³P und ¹D, i.e. the excited the carbon atom, are represented on the next illustration. To the right one can see the energy levels which are obtained by (2s) electron excitation.

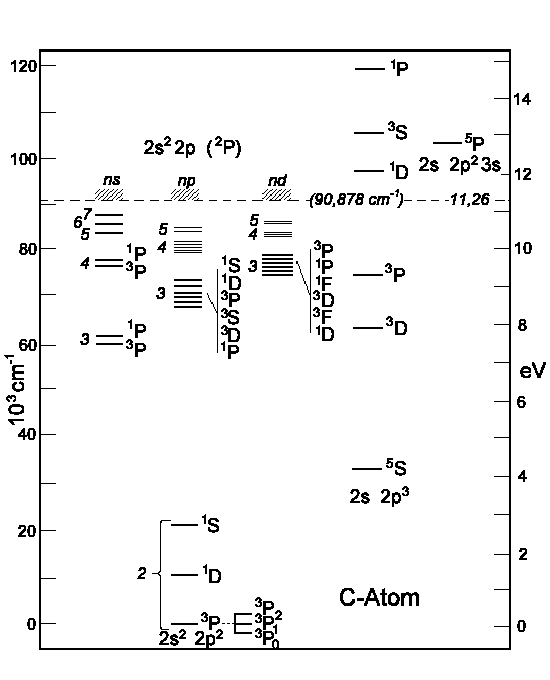Figure: Energy levels of Carbon atoms.
To the left: the (2p)-electron excitation.
To the right: the (2s)-electron excitation.

The ground state of C-atom is the combination of two (np)-electrons. The table below lists the terms for an atom with three (np)-electrons, i.e. p³ which leads to the states ⁴S, ²P and ²D.

Configuration	Term		Configuration	Term
s s² p, p⁵ p², p⁴ p³	²S ¹S ²P ¹S, ¹D, ³P ⁴S, ²P, ²D		d, d⁹ d², d⁸ d³, d⁷ d⁴, d⁶ d⁵	²D ¹S, ¹D, ¹G, ³P, ³F ²D, ²F, ²G, ²H, ⁴P, ⁴F ¹S, ¹D, ¹F,¹G,¹I,³P,³D,³F,³G,³H,⁵D ²S, ²P, ²D,²F,²G,²H,²I,⁴P,⁴D,⁴F,⁴G,⁶S

Nitrogen:
z = 7

n s p

L 2 Ýß Ý Ý Ý

K 1 Ýß N

(1s²) ( 2s²) ( 2p³)

According to Hunds rule spins should be directed as parallel to each other as possible. So that the total spin will be S = ³/₂. According to the above table 3 terms ⁴S, ²P, ²D is the combination of three p-electrons. And the state is:

⁴S_3/2

Oxygen:
z = 8

n s p

L 2 Ýß Ýß Ý Ý

K 1 Ýß O

(1s²) ( 2s²) ( 2p⁴)

The above-mentioned considerations would be very difficult to apply to this atom having 4 p-electrons: we will consider another way of 4 p-electrons combination here:

We've known that the shell is fulfilled with 6 p-electrons (p⁶) and also L = 0 and S = 0. We will represent our Oxygen atom as 2 electrons of (p⁶)-shell would be absent. Now these missing electrons or also holes are combined into "2-holes configuration" since holes have also spin ½. Therefore we have as for Carbon atom the following possible states ¹S, ³P, ¹D. The highest spin (Hunds rule (1)) is S = 1 i.e. ³P is the ground state and total kinetic moment J is for the ground state (Hunds rule (2)) J = L + S = 2. And finally:

³P₂

Fluorine:
z = 9

n s p

L 2 Ýß Ýß Ýß Ý

K 1 Ýß F

(1s²) ( 2s²) (2p⁵) : ²P_3/2

There is no one p-electron i.e. L = 1 and S = ½.

J = ½ and ³/₂ are possible. According to Hunds rule (2) the higher J-value is possible for the ground state:

²P_3/2

Neon:
z = 10

	n	s	p
L	2	Ýß	Ýß	Ýß	Ýß
K	1	Ýß		Ne

(1s²) (2s²) (2p⁶) : ¹S₀

2p-shell is full ! High ionization energy 21,6 eV.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.