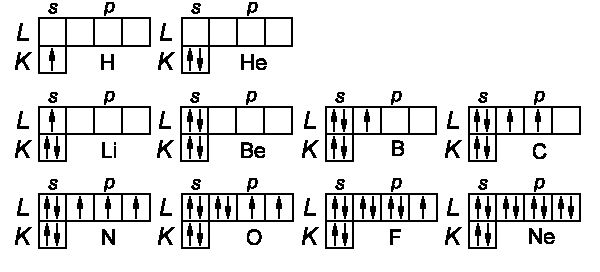

Hydrogen:
z = 1
| n |
|
| |||
| L | 2 | ||||
| K | 1 |
|
H | ||
One electron (1s), the ground state is 2S½
The
binding energy (Ionization energy) is 13,6 eV
Helium:
z = 2
| n |
|
| |||
| L | 2 | ||||
| K | 1 | Ýß | He | ||
2 electrons (1s) (1s), ground state 1s2
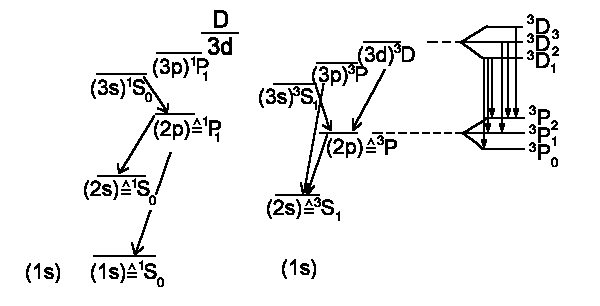
Since both electrons have the same main quantum numbers then the ground state should be 1S0 (total spin S = + ¯ = 0). If we excite an electron into n = 2, i.e. 2s state (1s) (2s) then both electrons have different main quantum numbers n and total spin can be S = 1. Here we show a rough scheme of Helium energy levels and possible transitions:
Lithium:
z
= 3
| n |
|
| |||
| L | 2 | Ý | |||
| K | 1 | Ýß | Li | ||
According to Pauli there is no 1s3 configuration but
1s2 2s º
2S½.
- fulfilled shell
with L = 0 and S = 0, J = 0.
If the nucleus has been covered fully by two 1s electrons then the ionization energy would be 13,6 eV/4 = 3,4 eV. Since the wavefunction of 2s electron penetrates deeper into the nucleus we therefore have a slightly higher ionization energy: 5,4 eV or Zeff = 1,3.
Since the 1s2 shell is fully occupied, we have a noble
gas configuration. Therefore, we sometimes write He(2s) for the Li-ground state
configuration. Another way is to use capital letters K, L, M, N.... for fully
occupied shells, or K(1s) for Li.
Beryllium:
z = 4
| n |
|
| |||
| L | 2 | Ýß | |||
| K | 1 | Ýß | Be | ||
(1s2) (2s2) ≡1S0
The binding energy would be 24,6 eV/4 = 6,2 eV (24,6 eV ≡ He). Because of wavefunctions'
penetration into the nucleus we have 9,3 eV. Thus Beryllium isn't as
chemically inert as He.
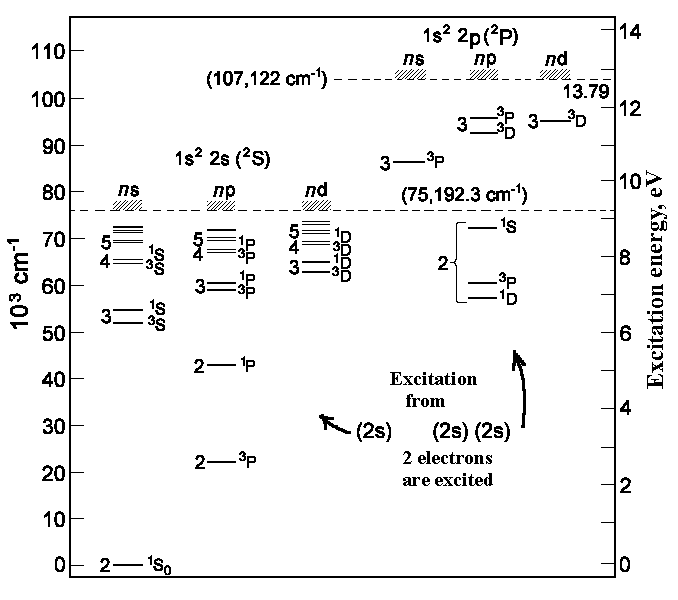 |
| Energy states of Beryllium |
Boron:
z =
5
| n |
|
| |||
| L | 2 |
|
Ý | ||
| K | 1 | Ýß | B | ||
(1s2) (2s2) (2p) ≡2P½
2P3/2 is also principally possible as the ground state. Nevertheless 2P½-state lies a bit lower energetically (Hunds rule (2)); this can be described as follows:
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.