Many-electron Systems

All atoms - except hydrogen and some ions of light elements - consist of
many electrons. It may seem unimportant to know features of one-electron systems
which were discussed in the last chapter. However, one-electron system
characteristics are very important to understand many-electron system
"functioning".
The first difficulty to describe many-electron system is the impossibility
to describe each particular electron motion since one must also pay attention to
interactions between electrons and electron-nucleus interaction. And therefore
the potential energy of the whole atom Ep is as follows:
Ep = all electronsS
− Ze²/4peori
+ all pairsS
e²/4peorij
(V.1)
The last sum corresponds to binding between electrons and that's why we
can't talk about particular movement of an electron independently of one
another. Each change in electron motion should influence on the motion of all
other electrons. That's why we can talk about the total energy of atom (or ion)
rather than particular energy of an electron. According to this reason we're
talking about the whole atom (or ion) wavefunction rather than the wavefunction
of an individual electron.
Many-electron problem can't be solved accurately; therefore there are some
approximations need to be applied. We will discuss these approximations on the
Helium atom example.
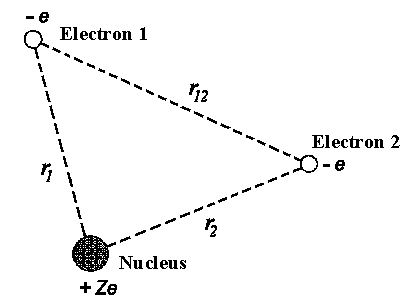 |
| Figure 1: Helium-like atom or ion. |
The two electrons atoms are the simplest ones among many-electron atomic
systems. For instance, negative hydrogen ion H−
(Z = 1), Helium atom He (Z = 2) and once ionized
Li+ ion (Z = 3) and so on. The potential energy of electrons is as
follows in this case (figure 1):
Ep = −
Ze²/4peor1
− Ze²/4peor2
+ e²/4peor12
(V.2)
The first two terms correspond to the attraction between nucleus and each of
the electrons and the last term corresponds to the interaction between two
electrons. Even for this extremely simple problem it's impossible to find
precise solution of Schroedinger equation: it's necessary to do some
approximations. Since the mathematical discussion of helium-like atoms exceeds
the bounds of this lecture we will be limited by quantitative description.
We can neglect the last term (or the elctron-electron interaction) in (V.2)
in the first approximation. It corresponds to the assumption that each electron
moves independently from all other electrons. This is so-called "Independent
particle model". Then we can describe electron motion by using hydrogen-like
wavefunctions ynlml
= Rnl(r) Ylml(θ,
φ) which are characterized by quantum numbers n, l, ml.
The energy of atom can be obtained from formula E = − RZ²/n²
(R: Rydberg constant = 13,6 eV) for the sum of particular electrons. That's why
the electronic motion energy would be then for Helium in the ground state n = 1 (Z = 2), EHe = 2 ·
(−54,4 eV) = − 108,8
eV (two electrons). The experimental value is another one: EHe
= − 78,98 eV. And so one can clearly see that our
first approximation gives energy lying too low. The reason is our neglect of
interaction between both electrons. It will give the increasing of atomic
energy.
We can improve our approximation by taking electron interaction into
account. Each electron is situated not only in the nuclear central field but
also in average central symmetrical field made by other electron. So the total
effect of each electron on the motion of another electron consists in the
covering of nuclear field. The atomic energy in the ground state is then as
follows:
E = 2(Z − δ)²
EH
where EH = −
13,6 eV (the energy of hydrogen-like motion) and δ
is the shielding constant which is equal to 0,32 for ground state of He in order
to match energy value with experimental measurements.
We would like to assign electrons as 1 and 2. Since we have assumed
electrons move independently of one another the detection probability of
electron 1 in one coordinate and electron 2 in other coordinate simultaneously
is equal to the product of probability distribution of individual electrons
since both events doesn't depend of each other: PAtom = P(1) P(2). We
can draw a conclusion here that the wavefunction in the independent particles
model should be a product of individual electron wavefunctions (this is a direct
consequence of Schroedinger equation for the system of independent particles).
If we assign the quantum numbers
(n, l, ml) of electron 1 as a and quantum
numbers of electron 2 as b then we will have:
yAtom = ya(1)
yb(2)
(V.3)
That finally gives the probability distribution:
|yAtom|² =
|ya(1) yb(2)|²
= |ya(1)|² |yb(2)|²
(V.4)
Due to the electron movement the average central field differs from 1/r-Coulomb field
which is produced by nucleus. It apparently demands light change of
wavefunctions ya(1)
and yb(2) that is not similar to
hydrogen-like wavefunctions. The change concerns the radial part Rnl
rather than angle part Ylml of the
wavefunction since force acting upon electrons is central force. Applying
corresponding mathematical methods one can optimize the electron wavefunction
and obtain the atomic energy states with quite good accuracy.
Even if we optimize the wavefunctions in (V.3) nevertheless this expression
couldn't be correct for the atomic wavefunction. Wavefunction (V.3) shows us
that electron 1 is in state a and electron 2 is in state b. But
the wavefunction
yAtom = ya(2)
yb(1)
(V.5)
corresponds to electron 2 in state a and electron 1 in state b
and it must describe the same energy state as the wavefunction in (V.3). The
fact that expressions (V.3) and (V.5) corresponds to wavefunctions of the same
energy is called exchange degeneracy.
Now electrons are identical and undistinguishable and we can only
talk concerning atom that one electron is situated in state a and another
one is in state b. It demands that wavefunction yAtom
and correspondingly |yAtom|²
(which corresponds to the probability distribution of both electrons) is
symmetric relative to both electrons namely both of them play the same role.
Neither wavefunction (V.3) nor (V.5) will comply with this demand. Nevertheless
we obtain appropriate wavefunction (which includes the mixture of electrons);
expressions (V.3) and (V.5) give rise to new above-mentioned appropriate
wavefunction:
yAtom = ya(1)
yb(2) ±
ya(2) yb(1)
(V.6)
In both cases (±) the expression for |yAtom|²
is symmetrical relative to both electrons.
We will call the wavefunction in expression (V.6) as the orbital
wavefunctions in the future since they describe the space or orbital behavior of
electrons in atom neglecting spin. The orbital wavefunction having positive sign
is as follows:
yS(1, 2) = ya(1)
yb(2) + ya(2)
yb(1)
(V.7)
which is symmetrical for two electrons and stays the same when exchanging by
electrons; i.e. yS(1,
2) = yS(2, 1). On the other
side there is another orbital wavefunction:
yA(1, 2) = ya(1)
yb(2) −
ya(2) yb(1)
(4.8)
this wavefunction is antisymmetrical for two electrons and changes its sign
when exchanging by electrons; i.e. yA(1,
2) = − yA(2,
1).
This symmetry behavior can be demonstrated by the following important
feature: the atomic energy which corresponds to yS
doesn't match with the energy corresponding to yA.
When the two electrons 1 and 2 are very close to each other then both
expressions are almost identical and therefore we have very small or zero
yA. That's why the antisymmetric
wavefunction yA describes the state in
which electrons don't come close to each other and have quite small average
repulsion energy. On the other hand, the symmetric wavefunction
yS
doesn't map out the opportunity that electrons could be very close to each other
at definite moments and therefore the average repulsion energy of
yS state is higher than that of
yA state. Here we have come to the following fact:
Helium-like atoms can be situated in two different
states which have different energies and different orbital atomic wavefunctions
yS
and yA having the same orbital quantum
numbers
a and b of both electrons in the independent particle model.
To put this another way, atom having two electrons possesses two different
stationary states and energy levels. One of these levels are described by using
symmetrical orbital wavefunctions and another one - by using antisymmetrical
orbital wavefunctions. This purely quantum mechanical effect follows from
undistinguished characteristic of an electron.
The only exception of the above-mentioned statement is the case when both
sets of orbital quantum numbers are identical; i.e.
a = b. It means that yA
= ya(1) ya(2)
− ya(2)
ya(1) = 0. If both electrons have
the same set of orbital quantum numbers then there will be only symmetrical
state possible.
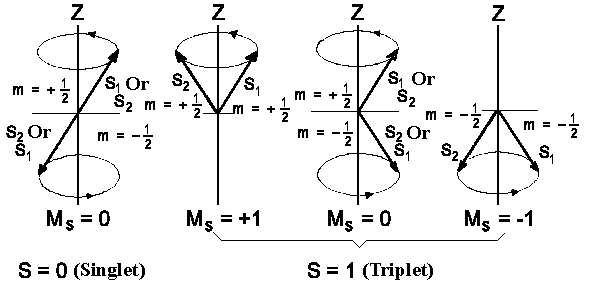 |
| Figure 2: Spin states of two electron system. |
We have considered only wavefunctions which describe the space distribution
of electrons, so far. The complete description of atomic state demands to take
electron spin into account. Each electron has spin ½. Spin of one
electron can be directed parallel or antiparallel relative to spin
of another electron; it gives the total spin (S = 1) or zero (S = 0) (capital
letters are used to assign the quantum numbers of total orbital kinetic moments
and small letters are used to mark corresponding values of individual particles).
Spin states with S = 0 are called Singlets which are
made up in a way shown on figure 2 (to the left). If however S = 1 the resulting
spin-vector can have three space orientations that are as follows, MS = +1, 0
and -1 correspondingly
(Figure 2, to the right). That's why spin-states having
S = 1 and three spin-wavefunctions belong to Triplets.
One can prove that the total spin-wavefunction for singlet-states (S = 0) is
antisymmetrical wavefunction, while the total spin-wavefunction of triplet-states (S = 1)
is symmetrical wavefunction. These spin-wavefunctions are assigned as
χ+, c-
for particular electrons:
| χA
= 1/Ö2
[χ+(1) c-(2)
− χ+(2)
c-(1)] |
MS = 0 |
| χS = |
ì
í
î |
χ+(1)
χ+(2) |
MS = +1 |
| 1/Ö2
[χ+(1) c-(2)
+ χ+(2) c-(1)] |
MS = 0 |
| c-(1) c-(2) |
MS = −1 |
The value MS = ms1 + ms2 of the component Sz
of the total spin is given for particular wavefunctions. The faktor 1/Ö2
is just for normalization. Resuming one can have:
Singlet-state (S = 0): antisymmetric spin-wavefunction χA
Triplet-state (S = 1): symmetric spin-wavefunction χS
We obtain the total atomic wavefunction by combining orbital wavefunctions
yS or yA
and spin-wavefunctions χS
or χA;
i.e.
ytotal = (orbital
wavefunction)
. (spin-wavefunction)
The ytotal symmetry depends obviously
on both factors symmetry. Since there are two types of orbital
wavefunctions and two types of spin-wavefunctions there are totally four
possible combinations. Now the helium energy levels study gives the following:
the symmetric orbital wavefunction yS
describes singlets (S = 0) and and therefore it corresponds to antisymmetric
spin-wavefunctions χA,
whereas the antisymmetric orbital wavefunctions yA
having triplets states (S = 1) correspond to symmetric spin-wavefunctions
χS. It's obviously that only the following
states are possible:
ytotal = (symmetric
orbital wavefunction) .
(antisymmetric spin-wavefunction)
= yS χA
Singlets
oder
ytotal = (antisymmetric
orbital wavefunction) .
(symmetric spin-wavefunction)
= yA χS
Triplets
ytotal is antisymmetric wavefunction
in any case since it's the product of antisymmetric and symmetric factors.
This statement can be written down in the following more general form for either
electron number:
| The total wavefunction of electron system should be
antisymmetric one. |

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.

