Russel-Saunders - vs. jj-Coupling

Our understanding of the behavior of an electron in a hydrogen atom lets us begin study of many-electron atoms.

The whole system functions properly because internal electrons making up the closed shell have zero total angular momentum and zero total spin. The effect of this closed shell, together with the nuclear potential of the external valence electrons, can be expressed by the central potential V(r). The Hamiltonian operator for the valence electrons then is as follows (we're neglecting the nuclear spin here):
 

Depending on strength of the last three terms, there are two boundary conditions:

1.)

The orbital angular momenta and spins are considered independently. The orbital anglular momentum _i of single electrons are then summed up to produce the total angular momentum:

and also the individual spins are summed up giving the total spin:

After that we have the weak spin-orbital interaction (H_sl) and the moments and  are summed up giving the total kinetic moment: 

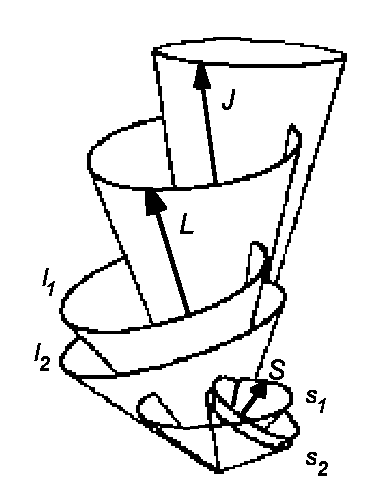
This type of coupling is also referred to as LS-Coupling or Russel-Saunders-Coupling (1925) and it holds true almost for all atoms (all light atoms).

The quantum numbers of Russel-Saunders-Coupling are orbital moment L, spin S, angular momentum J (nomenclature: ^2S+1L_J) and the magnetic quantum number M isn't clearly seen in this nomenclature. 
 

2.)

In this type of spin-orbital coupling, the interaction between spin of a single electron and spin _i + orbital moment _i of each other electron dominates giving the following total kinetic moment _i of i-electron:

The total kinetic moment of the atomic state is then as follows:

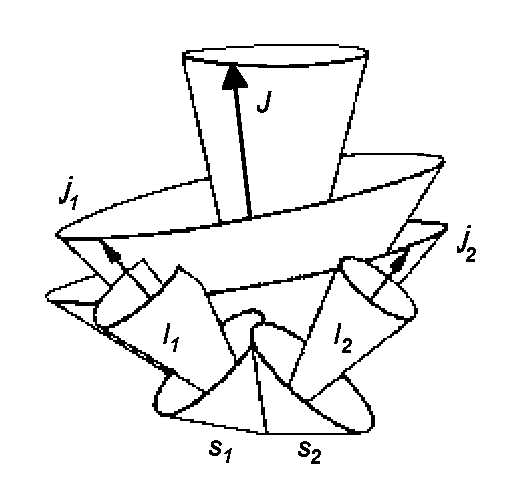
This type of coupling is called the jj-Coupling and it can be seen only in heavy atoms because of the great volume of the electronic shell that the valence electrons are situated in. Therefore, the interaction between valency electrons is weak compared with the spin-orbital interaction of a single electron. 

The quantum numbers are j_i     (nomenclature: (j₁, j₂, j₃, ...)_J)

To prevent from being misunderstood: the pure mathematical addition of vectors _i and _i gives the same result ; but only addition of  S_i and S_i and then      + ; and also _i + _i  and then S_i, correspondingly should show us the dominating interaction. The total kinetic moment is the conservative quantity for both LS- and jj-Coupling. 
 
 

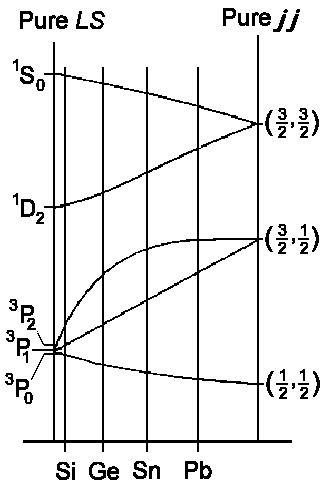jj - Coupling	Russel-Saunders- (LS-) Coupling	LS - jj Correlation for elements of the 4th main group

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.