A = aλ · b · c
where A is the measured absorbance, aλ is a wavelength-dependent absorptivity coefficient, b is the path length, and c is the analyte concentration. When working in concentration units of molarity, the Beer-Lambert law is written as:
A = el · b · c
where el is the wavelength-dependent molar absorptivity coefficient with units of M-1 cm-1. The λ subscript is often dropped with the understanding that a value for ε is for a specific wavelength. If multiple species that absorb light at a given wavelength are present in a sample, the total absorbance at that wavelength is the sum due to all absorbers:
A = (ε1 · b · c1) + (e2 · b · c2) + ...
where the subscripts refer to the molar absorptivity and concentration
of the different absorbing species that are present.
T = P/Po
where P is the power of light after it passes through the sample and Po is the initial light power. The relation between A and T is:
A = − log(T) = − log(P/Po)
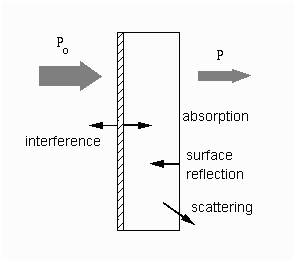
The figure shows the case of absorption of light through an optical filter and includes other processes that decreases the transmittance such as surface reflectance and scattering.

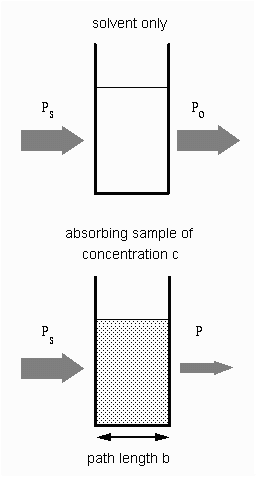
| In analytical applications we often want to measure the concentration
of an analyte independent of the effects of reflection, solvent absorption,
or other interferences. The figure to the right shows the two transmittance
measurements that are necessary to use absorption to determine the concentration
of an analyte in solution. The top diagram is for solvent only and the
bottom is for an absorbing sample in the same solvent. In this example,
Ps is the source light power that is incident on a sample, P
is the measured light power after passing through the analyte, solvent,
and sample holder, and Po is the measured light power after
passing through only the solvent and sample holder. The measured transmittance
in this case is attributed to only the analyte.
Depending on the type of instrument, the reference measurement (top diagram) might be made simultaneously with the sample measurement (bottom diagram) or a reference measurement might be saved on computer to generate the full spectrum. |
Absorption of light by a sample
 |
Modern absorption instruments can usually display the data as either
transmittance, %-transmittance, or absorbance. An unknown concentration
of an analyte can be determined by measuring the amount of light that a
sample absorbs and applying Beer's law. If the absorptivity coefficient
is not known, the unknown concentration can be determined using a working
curve of absorbance versus concentration derived from standards.
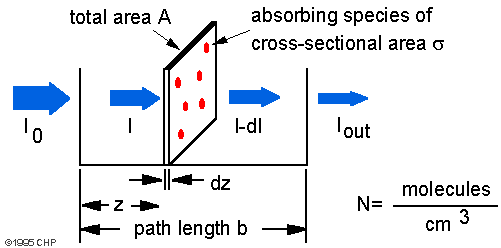
Io is the intensity entering the sample at z = 0, Iz is the intensity entering the infinitesimal slab at z, dI is the intensity absorbed in the slab, and I is the intensity of light leaving the sample. Then, the total opaque area on the slab due to the absorbers is σ · N · A · dz. Then, the fraction of photons absorbed will be σ · N · A · dz / A so,
dI/Iz = - s · N · dz
Integrating this equation from z = 0 to z = b gives:
ln(I) − ln(I0) = − σ · N · b
or
− ln(I/Io) = σ · N · b
Typical cross-sections and molar absorptivities are:
| σ (cm2) | ε (M-1 cm-1) | |
| absorption - atoms | 10-12 | 3x108 |
| absorption - molecules | 10-16 | 3x104 |
| absorption - infrared | 10-19 | 3x10 |
| Raman scattering | 10-29 | 3x10-9 |
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.