The hydrogen atom can occupy many different states that are characterized
by the familiar quantum numbers - n, l, s, ml, ms;
and each of these states has a characteristic spatial profile associated
with the wavefunction for this state. The wavefunction can be written (in
the bra and ket notation of Dirac) as:
< n, l, s, ml, ms >
so that all of the important quantum numbers appear. Sometimes the
wavefunctions are abbreviated as <x> just to save writing or to make
the wavefunction arbitrary. Some distributions corresponding to these wavefunctions
are:

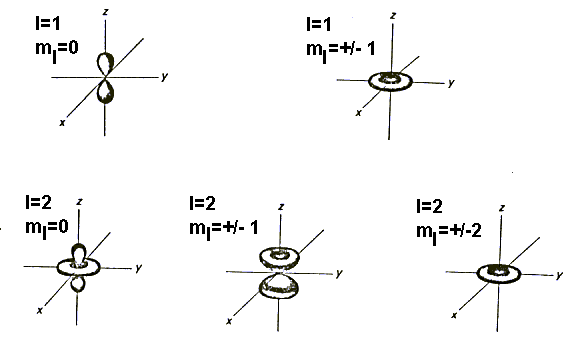
Try sketching the wavefunctions for l = 0, ml = 0; l = 1, ml = 0, +/-1; and l = 2, ml = 0, +/-1, +/-2
All of these wavefunction are stationary, i.e., they do not change in time. A technical way of saying the same thing is to say they are eigenfunctions of the time evolution operator which is the Hamiltonian of the system. The Hamiltonian is in fact the operator that describes the system. The eigenvalues of the Hamiltonian operating on the wavefunctions provide the energy of that state:
H < X > = E < X >
Any other operator that is compatible with the symmetry of the state will also have a eigenvalue characteristic of that state. The criteria that the operator by compatible is equivalent to saying the operator commutes with the Hamiltonian. The operator for the total momentum (J2) for example commutes if
H J2 - J2 H = [H, J2] = 0
If this is true, then both H and J2 can operate on a wavefunction to determine the eigenvalues simultaneously. Thus
J2 |S,L,J,Mj > = J(J+1) |S,L,J,Mj >
If one finds all of the operators and their corresponding eigenvalues that are compatible with the symmetry of the system (that is with the Hamiltonian that describes the system), the wavefunctions can be completely described. For atomic and molecular systems, there are an infinite number of states and each of them is characterized by their energy and angular momentum.
A very important part of quantum mechanics concerns what happens when one of these stationary states is perturbed by something. If an electric field is applied to a hydrogen atom, the electron clouds are distorted and polarized. Their shapes no longer correspond to the original wavefunctions and the symmetry of the system has been destroyed. Some of the operators that were previously compatible with the system (i.e. they commuted with the Hamiltonian) no longer commute and therefore the quantum numbers are no longer "good." Such a situation is sketched below
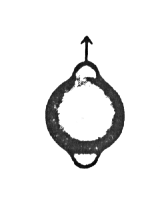
Try sketching an l = 0, ml = 0 orbital that is distorted in the vertical direction:
The wavefunctions for this new situation must be different from the original wavefunctions and yet they need not be very much different if the perturbation is small. Fortunately, one does not need to solve this new problem from scratch because any new wavefunction, even a distorted one, can be described by a linear combination of the old wavefunctions. This is possible because the old wavefunctions form a complete set. Thus the distorted electron cloud sketched above can be described by the following combination:
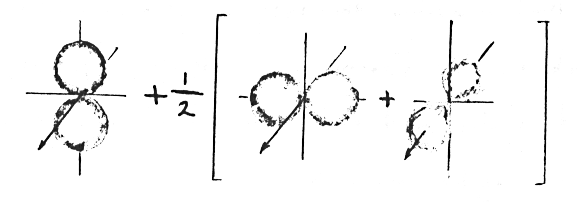
Mathematically, a new wavefunction < X > would be written in terms
of the old wavefunctions:
< Xn > (where n = 1,2,3,...)
< X > = summation over n of a(n) * < Xn >
where a(n) are coefficients that determine how much of each old wavefunction makes up the new wavefunction (or how much gets "mixed in"). Since the new wavefunction has a symmetry of its own, group theory can be used to tell what old states are compatible and can be mixed in.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.