Die Berechnung der Molekülorbitale nach Hückel
und die Ergebnisse werden anhand des Acrolein-Moleküls
erklärt (von Dr. Horst Bögel übernommen).
.
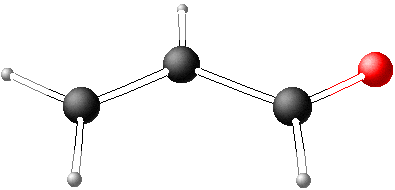
Als erster Schritt ist eine Säkulardeterminante
zu erstellen, die den Aufbau des Moleküls beschreibt.
Auf der Diagonale der Matrix befinden sich Atomparameter, wobei für Kohlenstoff x zu setzen ist und für evl. vorhandene Heteroatome X der Summenterm x+hX.
Für die C-C-Bindungen ist 1 (Eins) zu setzen und für C-X-Bindungen
der Parameter kC-X.
In der nachfolgenden Tabelle der Heteroatomparameter finden Sie die
meistens benötigte Werte für hX und kC-X
:
G. DERFLINGER, H. LISCHKA: Mh. Chemie 100 (1969) 1003
| X | hX | C-X | kC-X | |
|---|---|---|---|---|
| F | 2,84 | C-F | 0,68 | |
| Cl | 1,45 | C-Cl | 0,57 | |
| Br | 1,16 | C-Br | 0,38 | |
| J | 0,78 | C-J | 0,19 | |
| :O | 2,06 | C-O: | 1,31 | |
| :O-CH3 | 1,96 | C=O | 1,93 | |
| .O | 1,18 | C-N: | 1,30 | |
| :N | 1,47 | C=N. | 1,06 | |
| .N | 0,83 | C-CH3 | 0,18 | |
| :CH3 | 0,88 | N-O | 1,95 |
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | x | 1,0 | 0,0 | 0,0 |
| 2 | 1,0 | x | 1,0 | 0,0 |
| 3 | 0,0 | 1,0 | x | 1,93 |
| 4 | 0,0 | 0,0 | 1,93 | x+1,18 |
Der Determinantenwert führt auf eine Gleichung vierten Grades:
x4 + 1,18 x3 - 5,725x2 - 2,36x + 3,725 = 0
Die Nullstellen dieser Gleichung
x1 = -2,7654
x2 = -1,0207
x3 = 0,6880
x4 = 1,9182
ergeben die Eigenwerte.
Die Einelektronenergien ergeben sich aus der Gleichung:
Ej = α - xj β-
diese sind im folgenden Diagramm dargestellt. Empirisch ermittelt wurden für α= -11 eV und für β= -2,5 eV
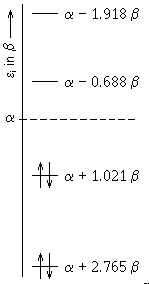
Die Gesamtenergie des Moleküls ergibt sich als Summe der Orbitalenergien, für die π-Elektronen-Energie E folgt somit:
E = Σj=1 bj Ej
bi als Besetzungszahl kann nur Werte 0, 1 und
2 annehmen.
Für das Acrolein-Molekül im Grundzustand beträgt die
π-Elektronen-Gesamtenergie
(4 π-Elektronen):
E = 2(α+2,7654β)+2(α+1,0207β) = 4α+7,5722β = -25,0695 eV
Σr=1 (hrs- Ei δrs) cir = 0
wenn Bindung r-s besteht, dann ist hrs = βrs, sonst ist hrs = 0 (Null).
αrs = 1 bei r=s, sonst Null.
Die Ergebnisse sind in der Tabelle zusammengestellt:
| MO 1 | MO 2
HOMO |
MO 3
LUMO |
MO 4 | |
|---|---|---|---|---|
| Eigenwerte | -2.7654 | -1.0207 | 0.6880 | 1.9182 |
| Atom1 | 0.0919 | -0.6593 | -0.6990 | -0.2613 |
| Atom2 | 0.2542 | -0.6730 | 0.4809 | 0.5012 |
| Atom3 | 0.6111 | -0.0276 | 0.3682 | -0.7002 |
| Atom4 | 0.7439 | 0.3341 | -0.3804 | 0.4362 |
Die einzelnen MO's sind unten dargestellt:
MO y12
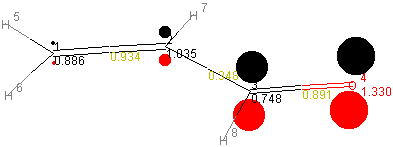
MO y22 (HOMO)
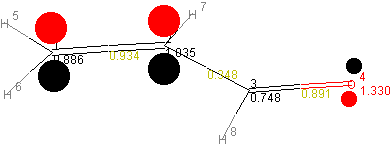
MO y30 (LUMO)
MO y40
| Besetzung: | y12 | y22 | y30 | y40 |
|---|
Mit den Formeln:
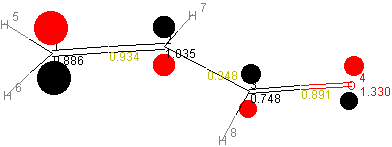
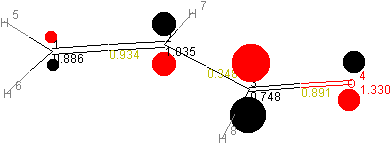
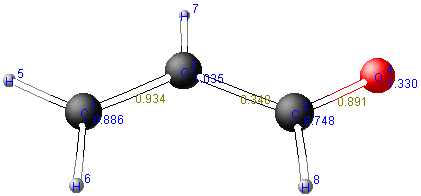
kann eine p-Matrix erstellt werden, anhand der sich ein Moleküldiagramm
konstruieren läßt.
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0.8863 | |||
| 2 | 0.9342 | 1.0351 | ||
| 3 | 0.0 | 0.3479 | 0.7485 | |
| 4 | 0.0 | 0.0 | 0.8909 | 1.3302 |
Die auf der Diagonale der p-Matrix liegenden Werte ergeben die
Elektronendichten (prr) an den einzelnen Atomen.
Beispiel: Elektronendichte am C(2)-Atom
Die Formalladung jedes Atoms beträgt: Qr = Nr - prr.
Aus den Nichtdiagonal-Werten der p-Matrix erhält man die
Bindungsordnungen (prs) zwischen den Atomen.
Beispiel: Bindungsordnung der C=O-π-Bindung
prs = 2 * (0,6111 * 0,7439) + 2 * (0,0276 * -0,3341) + 0 * (0,3682 * -0,3804) + 0 * (-0,7002 * 0,4362) = 0,8909
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.