In einem idealen Metall erstrecken sich die Bindungsorbitale über die gesamte Probe. Wir betrachten, der Einfachheit halber, eine unendlich lange Kette von Atomen, d.h. ein eindimensionales Metall, in der jedes Atom einzelne Valenzelektronen in einem s-Orbital hat. Die LCAOs des Metalls gewinnen wir, indem wir die Atome linear aneinanderreihen. Nach dem Aufbauprinzip ermitteln wir schließlich die Elektronenstruktur.
Bändermodell
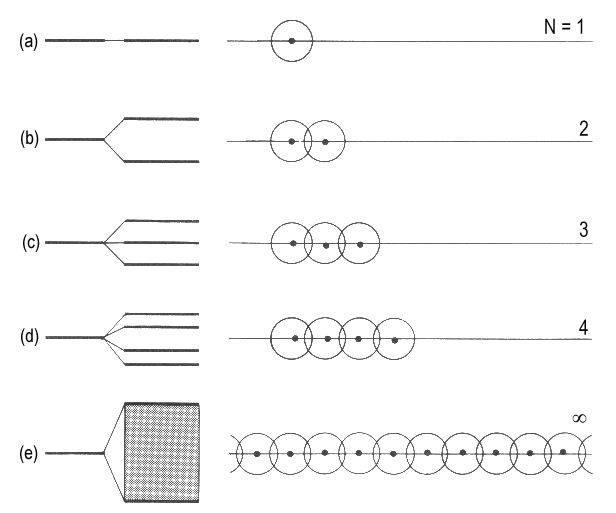 |
| Abb.1: Die Entstehung eines Bandes aus N Orbitalen beim schrittweise Anfügen von Atomen an eine Kette. Die Bandbreite bleibt endlich; das Band ist praktisch kontinuierlich, obwohl es eigentlich aus N verschiedenen Orbitalen besteht. |
Ein einzelnes Atom bringt ein s-Orbital mit einer bestimmten Energie
mit (Abb.1a). Wenn ein zweites Atom hinzukommt, so überlappt es mit
dem ersten Atom, und es entsteht ein bindendes und ein antibindendes Orbital
(Abb.1b). Das dritte Atom überlappt mit seinem unmittelbaren Nachbar
und ein wenig auch mit dem übernächsten, und aus diesen drei
Atomorbitalen entstehen drei MOs (Abb.1c). Wenn ein viertes Atom hinzukommt,
so wird ein viertes MO gebildet (Abb.1d). Wir können jetzt absehen,
was beim Hinzufügen weiterer Atome geschieht: Der von den MOs überdeckte
Energiebereich wird erweitert und mit immer mehr Orbitalen (für jedes
Atom eins mehr) aufgefüllt. Wenn man N Atome aneinanderreiht, dann
decken N Molekülorbitale ein Band endlicher Breite ab, und die Hückelsche
Säkulärdeterminante lautet
| |
| | | | | |
x | 1 | 0 | 0 | 0.... | 0 | |
| | | | | |
= 0 |
| 1 | x | 1 | 0 | 0.... | 0 | |||
| 0 | 1 | x | 1 | 0.... | 0 | |||
| : | : | : | : | : | : | |||
| : | : | : | : | : | : | |||
| 0 | 0 | 0 | 0 | 0.... | x |
Die Theorie der Determinnanten führt im Falle einer solchen symmetrischen tridiagonalen Determinante für die Wurzeln zu der Formel
E = α + 2 β cos{kπ/(N+1)} , k = 1, 2, ..... N
Wenn N unendlich groß ist, dann wird der Abstand zwischen benachbartnen
Energieniveaus (also zwischen den Niveaus für k und k+1) unendlich
klein, aber das Band hat eine endliche Breite (d.h. die Differenz
der Energien für k = N und k = 0 ist endlich und für N ®
¥ gleich −4β).
Wir wollen uns dieses Band aus N verschiedenen MOs aufgebaut vorstellen,
von denen das unterste (mit k = 0) voll bindend und das oberste ( mit k
= N) voll antibindend ist.
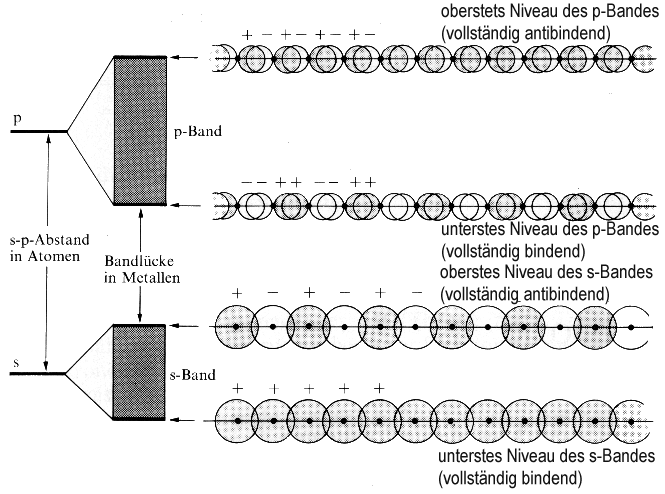 |
| Abb.2: Bei der Überlappung von s-Orbitalen entsteht ein s-Band, bei der Überlappung von p-Orbitalen ein p-Band. In dem hier gezeigten Fall ist der Abstand zwischen den s- und den p-Orbitalen der Atome so groß, dass zwischen den Bändern eine Lücke bleibt. In manchen Fällen ist der Abstand kleiner, so dass sich die Bänder überlappen. |
Das auf diese Weise durch (s, s)-Überlappung gebildete Band nennt
man auch s-Band. Wenn die Atome p-Orbitale haben, dann führt
uns dieselbe Überlegung zum p-Band (Abb.2). Liegen die p-AOs energetisch
höher als die s-AOs, dann liegt auch das p-Band höher als das
s-Band, und zwischen den Bändern kann ein Bereich ohne Energienivaus,
also eine Bänderlücke sein.
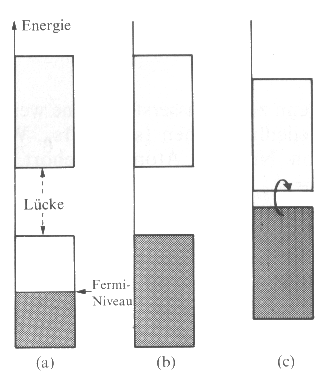 |
| Abb.3: (a) Wenn N Elektronen ein Band aus N Orbitalen besetzten, so ist das Band nur halb gefüllt, und die Elektronen in der Nähe des Fermi.Niveaus (am oberen Rand der besetzten Niveaus) bleiben beweglich. (b) Wenn 2 N Elektronen vorhanden sind, so ist das Band voll, und das Material ist ein Isolator. (c) Wenn die Lücke zwischen den Bändern schmal ist, kann ein Halbleiter vorliegen. Die elektrische Leitfähigkeit wird dann durch thermische Anregung der Elektronen oder auch durch Dotierung mit geeigneten Fremdatomen erzeugt. |
Sehen wir uns jetzt einmal die Elektronenstruktur eines Metalles an,
dessen Atome je ein Elektron beitragen (z.B. die Alkalimetalle). Dann gibt
es N Atomorbitale und folglich N Molekülorbitale, die in ein scheinbar
kontinuierliches Band gezwängt werden. N Elektronen sind unterzubringen,
deshalb werden nur die untersten ½ N Orbitale besetzt (Abb.3a).
Von besonderer Wichtigkeit ist hier, dass es unbesetzte Niveaus gibt,
die sehr dicht über dem obersten besetzten Niveau, dem Fermi-Niveau
liegen; man braucht deshalb nur sehr wenig Energie, um die obersten Elektronen
anzuregen. Ein Teil der Elektronen ist daher sehr beweglich; auf diese
Weise kommt die elektrische Leitfähigkeit zustande. Die elektrische
Leitfähigkeit ist ein Charakteristikum der nur teilweise gefüllten
Orbitalbänder.
Isolatoren und Halbleiter
Wenn jedes Atom zwei Elektronen beiträgt, dann haben wir 2 N Elektronen auf den N Orbitalen des s-Bandes unterzubringen. Das Fermi-Niveau liegt jetzt am oberen Rand des Bandes, dann kommt eine Lücke, bevor das nächste Band beginnt (Abb.3b). Das entspricht einem Isolator, denn die Elektronen sind nicht mehr beweglich. Ein Beispiel ist eine Kette von Heliumatomen in festem Helium. Bei den Elementen der 2.Gruppe überlappt das p-Band das s-Band; deshalb ist Beryllium ein elektrischer Leiter, denn für die Elektronen, die das 2s-Band gerade füllen, sind auch leere Orbitale des p-Bandes erreichbar.
Es gibt Materialien, die nur eine schmale Bandlücke haben (Abb.3c). Sie sind Nichtleiter, aber wenn einige Elektronen so weit angeregt werden, dass sie in das obere Band übergehen, dann kann elektrische Leitfähigkeit auftreten. Man nennt solche Materialien Halbleiter. Die Anregung der Elektronen kann auf verschiedene Weise erfolgen. Wenn die Lücke nicht breiter als etwa kT ist, dann kann man durch thermische Anregung genügend viele bewegliche Ladungsträger erzeugen, und man beobachtet bei einer Temperaturerhöhung eine Anstieg der Leitfähigkeit (In normalen Metallen nimmt die Leitfähigkeit bei Temperaturerhöhung ab). Auch durch Zugaben von bestimmten Verunreinigungen zu ansonsten ultrareinen Substanzen lassen sich Halbleiter-Effekte hervorrufen. Wenn die Verunreinigungen Elektronen einfangen, so entziehen sie diese Elektronen dem gefüllten Band; dabei entstehen Elektronenlücken, die den übrigen Elektronen auf dem Band eine gewisse Beweglichkeit ermöglichen. Man spricht in diesem Fall von Halpleitern vom p-Typ (die Löcher sind gegenüber den Elektronen in dem Band positiv). Andere Verunreinigungen (worunter wir uns nicht zwangsläufig eine unerwünschte Beimengung vorzustellen haben) können überschüssige Elektronen mitbringen (z.B. P-Atome in Germanium); diese Elektronen besetzten Bänder, die vorher leer waren, und führen zu Halbleitern vom n-Typ (das n weißt auf die negative Ladung der beweglichen Ladungsträger hin).
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.