Auswahlregeln bei Schwingungsübergängen

Die Intensität eines Vibrationsübergangs ist proportional zu |R_v|², dem Quadrat des Übergangsmoments der Vibration R_v, wobei gilt

R_v = òy_v'* µy_v'' dτ_v

Die Integration läuft über alle Schwingungskoordinaten. Offensichtlich gilt:

R_v = 0 für einen verbotenen Übergang
R_v ¹ 0 für einen erlaubten Übergang

An Hand einfacher Symmetrieüberlegungen kann man feststellen, ob das Integral von Null verschieden und damit ein Übergang erlaubt ist. Sind beide Vibrationszustände nicht entartet, muss der Integrand totalsymmetrisch sein:

G(y_v') xG(µ) xG(y_v'') = A

Hier steht G wieder für "irreduzible Darstellung von". A entspricht der totalsymmetrischen Darstellung einer beliebigen, nicht-entarteten Punktgruppe. Die Gleichung muss modifiziert werden, wenn mindestens einer der beiden Vibrationszustände entartet ist:

G(y_v') xG(µ) xG(y_v'') É A

Das Boolsche Symbol É bedeutet "enthält". Zum Beispiel enthält E x E die irreduzible Darstellung A₁, also

E x E É A₁.

Das Übergangsmoment ist ein Vektor und kann in seine Komponenten entlang der x-, y- und der z-Achse zerlegt werden:

R_v,x = òy_v'* µ_xy_v'' dτ_v;

R_v,y = òy_v'* µ_yy_v'' dτ_v;

R_v,z = òy_v'* µ_zy_v'' dτ_v

Es gilt:

|R_v|² = (R_v,x)² + (R_v,y)² + (R_v,z)²

Daher ist ein Übergang v' - v'' erlaubt, wenn eine der Komponenten R_v,x, R_v,y oder R_v,z von Null verschieden ist.

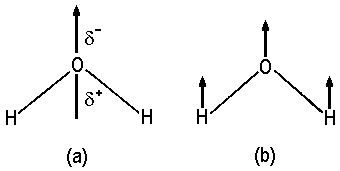Abb. 1: (a) Vektor des Dipolmomentes von H₂O und (b) Translation des Moleküls in dessen Richtung.

Das Dipolmoment ist ein Vektor mit einer bestimmten Richtung. Es hat daher die Symmetrieeigenschaften einer Translationsbewegung in dieselbe Richtung. In Abb. 1 gleicht die Symmetrie des Dipolmomentes eines Wassermoleküls und die Translation des gesamten Moleküls in Richtung des Dipolmoments. Wir sehen, dass beide zur selben irreduziblen Darstellung gehören, nämlich der totalsymmetrischen Darstellung A₁. Ganz allgemein gilt

G(µ_x) = G(T_x);

G(µ_y) = G(T_y);

G(µ_z) = G(T_z)

T_x, T_y und T_z bezeichnen die auf cartesische Koordinaten bezogenen Komponenten des Translationsvektors. Wir erhalten daher:

G(y_v') xG(T_x) xG(y_v'') = A und / oder G(y_v') xG(T_y) xG(y_v'') = A und / oder G(y_v') xG(T_x) xG(y_v'') = A

Durch "und/oder" wird angedeutet, dass für einen erlaubten Übergang eine oder mehrere Komponenten von R_v von Null verschieden sein können.

Häufig wird der untere Zustand eines Übergangs der Schwingungsgrundzustand mit v'' = 0 sein. Die Wellenfunktion dieses Zustands ist totalsymmetrisch, G(y_v'') = A, und die Gleichungen vereinfachen sich zu

G(y_v') xG(T_x) = A

und / oder G(y_v') xG(T_y) = A und / oder G(y_v') xG(T_z) = A

denn die Multiplikation mit der totalsymmetrischen Darstellung läßt alles unverändert. Ergibt die Multiplikation zweier Darstellungen die totalsymmetrische Darstellung, so sind diese beiden Darstellungen identisch. Es folgt daher

G(y_v') = G(T_x) und/oder G(T_y) und/oder G(T_z).

Das ist die Auswahlregel für einen Schwingungsübergang vom Zustand v'' = 0 in einen beliebigen anderen Zustand einer nicht-entarteten Grund-, Ober- oder Kombinationsschwingung. Auch für den Übergang vom Zustand v'' = 0 in einen entarteten Zustand kann eine analoge Auswahlregel formuliert werden:

G(y_v') ÉG(T_x) und/oder G(T_y) und/oder G(T_z).

Für ein bestimmtes Molekül lassen sich also die Auswahlregeln nach folgendem Schema finden:

Punktgruppe des Moleküls bestimmen
irreduzible Darstellung der Translation der entsprechenden Punktgruppe nachschauen;
ausgehend vom Zustand v'' = 0 muss für erlaubte Übergänge gelten:

G(y_v') = G(T_x) und/oder G(T_y) und/oder G(T_z)

Mit Hilfe der Charaktertafel der C_2v-Punktgruppe können wir sofort die erlaubten Übergänge mit dem Zustand v'' = 0 aufschreiben:

A₁ − A₁;

B₁ − A₁;

B₂ − A₁.

Diese Übergänge sind entlang der z-, x- bzw. y-Achse polarisiert. Das bedeutet, dass z.B. bei dem Übergang B₁ − A₁ ein oszillierender elektrischer Dipol entlang der x-Achse induziert wird.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.