Walsh hat (nach Mulliken) gezeigt, wie man für Moleküle im
Grundzustand und in verschiedenen angeregten Zuständen auf die Gleichgewichtsgeometrie
schließen kann, wenn man die Abhängigkeit der Orbitalenergien
von der Geometrie diskutiert. Man spricht von den Walshschen Regeln oder
Walshschen Diagrammen.
 |
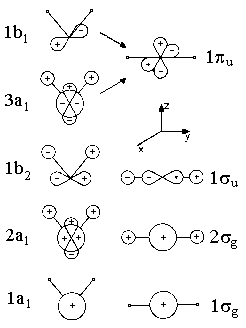 |
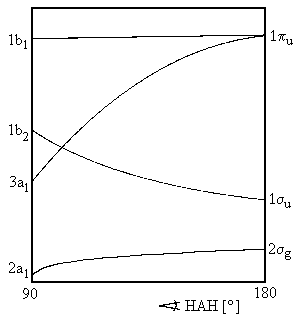
| Abb. 1: Walsh-Diagramm für AH2-Moleküle | Abb. 2: Schematische Darstellung der MO's in AH2-Molekülen |
In Abb. 1 sind, nicht maßstabsgetreu, Orbitalenergien als Funktion des Valenzwinkels für beliebige AH2-Moleküle aufgetragen (die beiden AH-Abstände sind als gleich angenommen). Die MO's, die aus AO's der K-Schale (bzw. bei Atomen der höheren Perioden aus der inneren Schalen) gebildet sind, wurden bewußt weggelassen, es werden also nur die Valenz-MO's betrachtet. Die in Abb. 1 dargestellte Abhängigkeit der Orbitalenergien vom Valenzwinkel entspringt nicht quantenchemischen Rechnungen, sondern allgemeinen, mehr qualitativen Überlegungen.
In der danebenstehenden Abb. 2 ist angegeben, wie die MO's qualitativ aussehen, d.h. aus welchen AO's sie aufgebaut sind. Zur Klassifizierung benutzen wir die In Kapitel IV eingeführten gruppentheoretischen Symbole, die uns das Symmetrieverhalten der MO's angeben, wie a1, b2 etc. Für einen Bindungswinkel 180°, also speziell für lineare Moleküle, benutzen wir die Symbole σg, σu etc. MO's des gleichen Symmetrietyps werden wie üblich durch eine Zahl vor dem Symbol gezählt, z.B. 1b1, 2b1 etc. Wir nutzen im folgenden nur aus, dass eine Klassifizierung nach Symmetrietypen möglich ist, sowie bei Symmetrieerniedrigung (z.B. Abknicken eines linearen Moleküls) eine Entartung von Orbitalen aufgehoben werden kann.
Die energetische Reihenfolge der MO's wird durch die energetische Reihenfolge der beteiligten AO's und dadurch, wieweit sie bindend oder antibindend sind, bestimmt.
Was ändert sich nun, wenn man das Molekül abknickt? Das im linearen Fall entartete πu-Orbital spaltet jetzt in zwei Komponenten auf, eine hat eine Knotenebene in der Molekülebene, die andere senkrecht zu dieser Ebene. Die Energie der zur Molekülebene antisymmetrischen Komponente (1b1) - es handelt sich im wesentlichen um ein p-AO des Zentralatoms, also ein nichtbindendes MO - wird von der Deformation des Moleküls weitgehend unabhängig sein, während die andere Komponente (3a1) bei Verkleinerung des Winkels bindend wird, da die Überlappung zunimmt und so die Orbitalenergie absinkt.
Das liegt daran (vergl. die schematische Darstellung der MO's in Abb. 2), dass im linearen Molekül die Überlappung des AO's 2pz von A mit der 1s-AO's der H-Atome verschwindet, dass die Überlappung und damit die Ausbildung einer Dreizentrenbindung aber um so günstiger wird, je kleiner der Bindungswinkel ist. Andererseits wird das im linearen Fall stark bindende MO 1σu bei Verbiegung (1b2) schwächer bindend, weil das 2py-Orbital im linearen Fall stärker mit den AO's der H-Atome wechselwirken kann. Die Energie des tiefsten Valenz-MO's sinkt also, wenn man das Molekül abknickt.
Haben wir jetzt 1 oder 2 Valenzelektronen zur Verfügung, so besetzten diese das 2σg- bzw. 2a1-Orbital. Dieses Orbital ist stabiler (wenn auch nicht in der Walshschen Originalveröffentlichung) bei einem Winkel < 180°, und das Molekül ist daher gewinkelt:
Beispiele für n = 1 oder 2Das nächste Elektron kommt in 1σu (1b2), dieses bevorzugt lineare Anordnung. Diese Tendenz setzt sich bei 3 Elektronen noch nicht, wohl aber bei 4 Elektronen durch:
H3+ α = 60°
LiH2+ α = 21,1°
Beispiele für n = 3 oder 4Das BeH2+ (n = 3) bedarf einer etwas eingehenderen Kommentierung. Es ist zwar experimentell nicht beobachtet worden (ebensowenig wie das BeH2), aber es existieren recht zuverlässige Rechnungen. Gehen wir davon aus, dass die Energie das 2a1-MO bei Abknickung sinkt, während die von 1b2 steigt und sich in der Nähe von 90° mit dem von 3a1 überkreuzt. Das bedeutet nicht nur, das wir abgeknickte Strukturen erwarten, sondern auch, dass die Grundkonfiguration bei größeren und kleineren Winkeln verschieden ist.
BeH2+ = 20 ° bzw. 73°
BeH2 = 180°
BH2+ = 180°
| große Winkel: | (2a1)21b2 | entspr. | 2B2 |
| kleine Winkel: | (2a1)23a1 | entspr. | 2A1 |
Zwei Zustände 2B2
und 2A1 konkurrieren also miteinander. Zu beiden
Zuständen gehören aufgrund verschiedener Gesamtsymmetrien voneinander unabhängige Potentialhyperflächen. Beide besitzen ein Minimum wobei SCF-Rechnungen folgende Gleichgewichtsgeometrien ergeben:
| 2A1 | 2B2 | |
| Ð HBeH | 20° | 73° |
| r Be-H | 4,43 a0 | 2,63 a0 |
| r H-H | 1,52 a0 | 3,14 a0 |
Im 2B2-Zustand liegt eine echte chemische Dreizentrenbindung vor (das Molekül ist grob gesagt ein gleichseitiges Dreieck), die Energie dieses Moleküls liegt zwar um etwa 150 kJ/mol über der Summe der Energien von Be+ (1s2 2s) und H2. Allerdings ist es gegenüber dieser Dissoziation stabil (mit einer Bindungsenergie von etwa 290 kJ/mol). In diesem 2B2-Molekül reicht gewissermaßen der Energiegewinn durch Bindung nicht aus, die Promotionsenergie vom Be+-Grundzustand in seinen Valenzzustand aufzubringen. Trotzdem ist eigentlich dieser Zustand des Moleküls mit den anderen AH2-Molekülen im Sinne der Walshschen Regel zu vergleichen. Der 2A1-Grundzustand entspricht eigentlich nicht einem BeH2+-Molekül, sondern einem losen Komplex zwischen Be+ und H2.
Das neutrale BeH2 ist, wie nach den Walshschen Regeln zu erwarten, im Grundzustand linear symmetrisch und hat einen Be-H Abstand von 2,53 a0. Es hat die Grundkonfiguration 1σg2 2σg2 1σu2. Die Tatsache, dass jetzt 4 Elektronen in bindenden MO's sind (2σg und 1σu) vgl. mit ca. nur 3 Elektronen im BeH2+, führt zu einer erhöhten Stabilität und in der Tat is BeH2 mit ca. 630 kJ/mol gegenüber Be + 2H gebunden und liegt auch energetisch ca. 170 kJ/mol tiefer als Be + H2 in ihren Grundzuständen. Daß BeH2 dennoch experimentell nicht beobachtet wurde, liegt seiner Fähigkeit, sich über Elektronenmangel-Wasserstoffbrücken zu polymerisieren.
BeH2 und das isoelektronische BH2+ haben vier Valenzelektronen. In Molekülen wie BH2 oder CH2 mit fünf bzw. sechs Valenzelektronen besetzen das fünfte und sechste Valenzelektron im Sinne der Walshschen Diagramm das 3a1-Orbital, das gewinkelte Anordnung bevorzugt. In der Tat sind Moleküle mit fünf oder sechs Valenzelektronen gewinkelt.
Beispiele für n = 5 oder 6:Ein siebentes oder achtes Elektron besetzt das Orbital 1b1. Diesem ist es gewissermaßen gleich, welchen Winkel das Molekül einnimmt, so dass auch Moleküle mit sieben oder acht Valenzelektronen gewinkelt sind.BH2 α = 131°
CH2 (Singulett) α = 102°
CH2 (Triplett) α = 136°
Beispiele für n = 7 oder 8:Das CH2 ist ein besonderer Fall. In der linearen Anordnung ist das Energieniveau 1πu nur doppelt besetzt, hat aber Platz für vier Elektronen. Also liegt eine offenschalige Konfiguration vor, zu der mehrere Terme gehören (genau wie bei der O2-Grundkonfiguration), und zwar 3Σg−, 1Δg, 1Σg+. Nach der Hundschen Regel ist das Triplett 3Σg− am tiefsten. Wenn wir das Molekül etwas abknicken, ändern sich die Terme: 3Σg− geht in 3B1 über, 1Δg spaltet in zwei Terme auf, nämlich 1A1 und 1B1, während 1Σg+ in 1A1 übergeht. Bei Winkeln nahe 180° liegt also sicher 3B1 im Sinne der Hundschen Regel am tiefsten. Dies ist solange schlüssig, wie die Termaufspaltung der Elektronenwechselwirkung größer als die Aufspaltung des 1πu-Niveaus als Folge der Symmetrieerniedrigung ist. Bei kleinen Winkeln, wo diese Aufspaltung des 1πu-Niveaus, d.h. der Abstand zwischen 3a1 und 1b1, größer ist als die Energie der Termaufspaltung, gilt das Aufbauprinzip. Man hat sechs Elektronen zur Verfügung und wird diese auf die MO's 2a1, 1b2, 3a1 verteilen. Da nur abgeschlossene Schalen vorliegen, ergibt sich ein totalsymmetrischer Zustand, d.h. ein 1A1-Term.NH2 α = 103,4°
OH2 α = 104,5°
Ob nun tatsächlich der durch die Hundsche Regel bevorzugte 3B1-Term
(bei seinem günstigen Winkel) oder der vom Aufbauprinzip geforderte
1A1-Term
(bei seinem günstigen Winkel) energetisch tiefer liegt, d.h. der Grundzustand
des CH2 ist, läßt sich durch eine qualitative Argumentation
nicht entscheiden. Der Energieunterschied zwischen beiden ist recht klein,
und zwar findet man durch ab-initio Rechnungen (siehe Abb. 3), dass
der Grundzustand 3B1 besitzt.
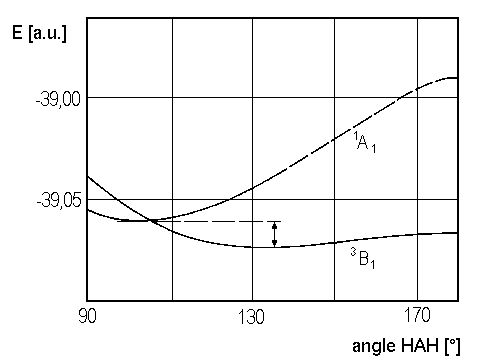 |
| Abb. 3: Potentialkurven der tiefsten Zustände des CH2, nach V. Staemmler [Theoret. Chim. Acta 31, 49 (1973)] |
Aus dem Walsh-Diagramm kann man aber entnehmen, dass der 3B1-Zustand mit der (offenschaligen) Konfiguration 2a12 1b22 3a1 1b1 sicher einen größeren Gleichgewichtswinkel (nahe 180°) als der 1A1-Zustand mit der Konfiguration 2a12 1b22 3a12 haben wird, weil die Besetzung von 1b1 statt 3a1 lineare Anordnung bevorzugt. Genauere Rechnungen ergeben die oben angeführten Gleichgewichtswinkel für 3B1 und 1A1. Die Potentialkurven der beiden tiefsten Zustände von CH2 sind in Abbildung 3 dargestellt.
Zusammengefaßt lauten die Walshschen Regeln für die Geometrie
der Grundzustände von AH2-Molekülen:
| 1- 3 Valenzelektronen: | gewinkelt |
| 4 Valenzelektronen: | linear |
| 5 Valenzelektronen: | schwach gewinkelt |
| 6 - 8 Valenzelektronen: | gewinkelt |
| 9 Valenzelektronen: | schwach gewinkelt |
| 10 - 12 Valenzelektronen: | linear |
Die Fälle 9 - 12 Valenzelektronen sind dabei nur von theoretischen Interesse, weil es dafür keine Beispiele gibt. Das hypothetische NeH2 hätte 10 Valenzelektronen.
Tabelle 1: Beispiele für MO's Besetzungen und daraus folgende
Geometrie nach Walshdiagrammen (α:
Bindungswinkel)
|
|
Molekül | a |
|
|
|
|
LiH2+ | 21.1° | 1Σg: 2σg2 | 1A1: 2a12 |
|
|
BeH2+ | 73° | 2Σu: 2σg2 1σu | 2B2: 2a12 1b2 |
|
|
BeH2 | 180° | 2Σg: 2σg2 1σu2 | 1A1: 2a12 1b22 |
| BH2+ | 180° | 2Σg: 2σg2 1σu2 | 1A1: 2a12 1b22 | |
|
|
BH2 | 131° | 2Πu:1σu2 1πu | 1A1: 1b22 3a1 |
|
|
3CH2 | 136° | 3S: 1σu2 1πu2 | 3B1: 1b22 3a1 1b1 |
| 1CH2 | 102° | 1S,1D:1σu2 1πu2 | 1A1: 1b22 3a12 | |
|
|
NH2 | 103.4° | 2Πu:1σu2 1πu3 | 2B1: 3a121b1 |
|
|
OH2 | 104.5° | 1Σg: 1σu1 1πu4 | 1A1: 3a12 1b12 |
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.