Ground State of a Diatomic Molecule

Introduction

Two atoms that can form a bond will do so to create a diatomic molecule when they approach each other closely. We describe the energy minimum with a potential energy curve, called a potential well.

Morse Potential

The potential energy, V(R), of a diatomic molecule can be described by the Morse potential:

V(R) = D_e (1 − 2^-b(R-Re))

where D_e is the well depth, R is internuclear distance, R_e is the equlibrium internuclear distance (bond length), and

β = pn_eÖ(2m/D_e)

ν_e is the vibrational constant and µ is the reduced mass.

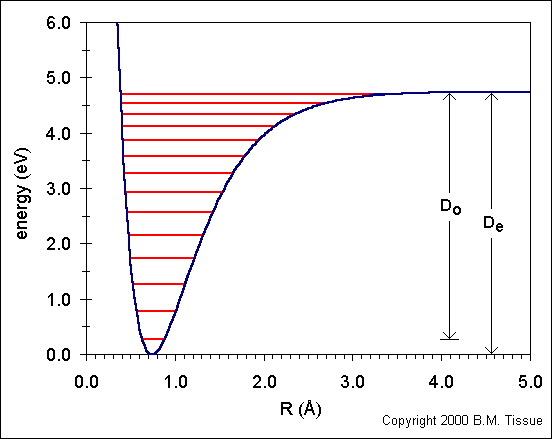
The following figure shows the ground state potential well of the H₂ molecule. The curve is calculated from the Morse potential and the energy levels are calculated using the harmonic oscillator model with the first anharmonic correction.

morse potential

D_o is the dissociation energy, which is slightly different from the well depth, D_e. The vibrational energy levels in this plot are calculated from:

Ev = (v + ½) ν_e - (v + ½)² ν_ex_e + (v + ½)³ ν_ey_e + higher terms

where v is the vibrational quantum number, v = 0,1,2,..., and x_e and y_e are the first and second anharmonicity constants, respectively. The v = 0 level is the vibrational ground state.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.