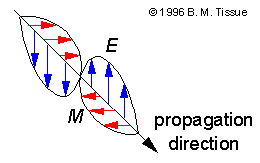
| Electromagnetic radiation consists of discrete packets of energy, which we call photons. A photon consists of an oscillating electric field component, E, and an oscillating magnetic field component, M. The electric and magnetic fields are orthogonal (perpendicular) to each other, and they are orthogonal to the direction of propogation of the photon. The electric and magnetic fields of a photon flip direction as the photon travels. We call the number of flips, or oscillations, that occur in one second the frequency, ν. Frequency has the units of oscillations per second, or simply s-1 (this unit is given the name Hertz). If the electric and magnetic fields of a photon could be recorded as the photon traveled some distance, it would leave the trail of E and M fields shown in the figure. |  |
All photons (in a given, non-absorbing medium) travel at the same velocity, v. The physical distance in the direction of propogation over which the electric and magnetic fields of a photon make one complete oscillation is called the wavelength, λ, of the electromagnetic radiation. The figure above shows the hypothetical history of a photon that has traveled the distance of one wavelength. The relationship between the light velocity, wavelength, and frequency is:
v = λ · ν
The electromagnetic nature of all photons is the same, but photons can have different frequencies. The names we give electromagnetic radiation for different wavelength and frequency ranges are listed in the electromagnetic spectrum document. The energy, E, of one photon depends on its frequency of oscillation:
E = h ν = hv/λ
where h is Planck's constant (6.62618x10-34 J·s).
c = λ · ν
When light passes through other media, the velocity of light decreases. Since the energy of a photon is fixed, the frequency of a photon does not change. Thus for a given frequency of light, the wavelength must decrease as the velocity decreases.
The decrease in velocity is quantitated by the refractive index, n, which is the ratio of c to the velocity of light in another medium, v:
n = c / v
| Since the velocity of light is lower in other media than in a vacuum,
n is always a number greater than one. The table lists the refractive index
of several examples. Refractive index is an intrinsic physical property
of a substance, and can be used to monitor purity or the concentration
of a solute in a solution. The refractive index of a material is measured
with a refractometer, and is usually made versus air. If the precision
warrants, the measurements can be corrected for vacuum. Note that the difference
between nair and nvacuum is only significant in the
fourth decimal place.
For anisotropic materials, such as quartz crystals, light of different polarizations (see below) will experience different refractive indices. These indices are called the ordinary refractive index, no, and the extraordinary refractive index, ne. |
|
Linearly (or plane) polarized light is light in which the electric-field vector is oscillating in only one direction. Linearly polarized light is produced by isolating one orientation of the electric field with a polarizer, or from lasers that contain polarized optical components.
Circularly polarized light is light in which the electric field vector
is rotating around the axis of light propogation. The electric field vector
can rotate in either the right or left direction (as viewed in the direction
of light propogation), and the light is called right circularly polarized
or left circularly polarized, respectively.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.